
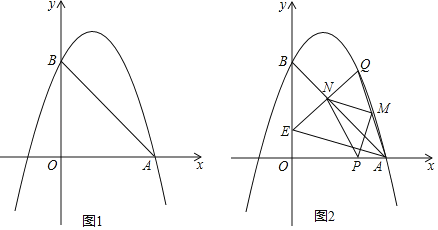
【题目】如图,抛物线y=﹣x2+bx+c与x轴正半轴交于A点,与y轴正半轴交于B,直线AB的解析式为y=﹣x+3.
(1)求抛物线解析式;
(2)P为线段OA上一点(不与O、A重合),过P作PQ⊥x轴交抛物线于Q,连接AQ,M为AQ中点,连接PM,过M作MN⊥PM交直线AB于N,若点P的横坐标为t,点N的横坐标为n,求n与t的函数关系式;
(3)在(2)的条件下,连接QN并延长交y轴于E,连接AE,求t为何值时,MN∥AE.
【答案】(1)y=﹣x2+2x+3;(2)Nx=3﹣![]() =
=![]() (0<t<3);(3)2.
(0<t<3);(3)2.
【解析】
(1)求出A、B两点坐标,利用待定系数法即可解决问题;
(2)如图1中,过点M作MG⊥x轴于G,NH⊥GM,于H.首先证明N、P、A三点在以M为圆心MA为半径的⊙M上,再根据△NMH≌△MPG,得到NH=MG,HM=PG,即可解决问题;
(3)如图2中,MN∥AE,QM=MA,得EN=QN,利用中点坐标公式,列出方程即可解决问题.
解:(1)∵直线AB的解析式为y=﹣x+3,
∴A(3,0),B(0,3),
∵抛物线y=﹣x2+bx+c经过A点,B点,
∴![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3;
(2)如图1中,过点M作MG⊥x轴于G,NH⊥GM,于H,
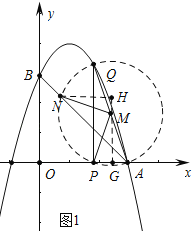
∵OA=OB,∠AOB=90°,
∴∠PAN=45°,
∵∠NMP=90°,
∴∠PAN=![]() ∠NMP,
∠NMP,
∴N、P、A三点在以M为圆心MA为半径的⊙M上,
∴MN=MP,
∵∠NHM=∠PGM=∠NMP=90°,
∴∠NMH+∠PMG=90°,∠PMG+∠MPG=90°,
∴∠NMH=∠MPG,
∴△NMH≌△MPG,
∴NH=MG,HM=PG,
∵P(t,0),
∴Q(t,﹣t2+2t+3),M(![]() ,
,![]() ),
),
∴PG=MH=![]() ﹣t=
﹣t=![]() ,HG=
,HG=![]() +
+![]() =
=![]() ,
,
∴Ny=![]() ,
,
∵点N在直线AB上,
∴Ny=﹣Nx+3,
∴Nx=3﹣![]() =
=![]() (0<t<3);
(0<t<3);
(3)如图2中,
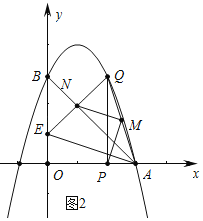
∵MN∥AE,QM=MA,
∴EN=QN,
∴![]() =
=![]() ,
,
∴t2﹣2t=0,
解得t=2或0(舍弃),
∴t=2时,MN∥AE.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=![]() ,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )
,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )

A. 2 ![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象交于点
)的图象交于点![]() .
.![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() . 一次函数的图象分别交
. 一次函数的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、点
、点![]() ,且
,且![]() ,
,![]() .
.
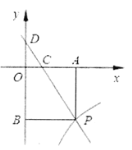
(1)求点![]() 的坐标;
的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当![]() 取何值时,一次函数的值小于反比例函数的值?
取何值时,一次函数的值小于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
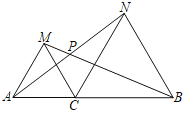
【题目】如图,点C为线段AB上一点,△ACM与△CBN都是等边三角形,AN与MB交于P.
(1)求证:AN=BM;
(2)连接CP,求证:CP平分∠APB.
查看答案和解析>>
科目:初中数学 来源: 题型:
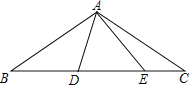
【题目】如图,在△ABC中,AB=AC=2![]() ,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为________.
,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
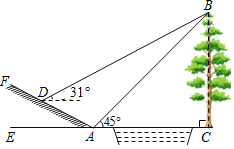
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)大树BC的高度约为多少米?(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
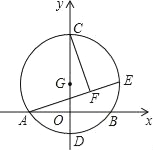
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
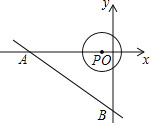
【题目】如图,直线y=-![]() x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是_______.
x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
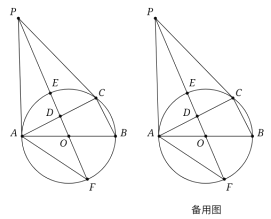
(1)证明:EF2=4ODOP;
(2)若tan∠AFP=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com