
【题目】如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
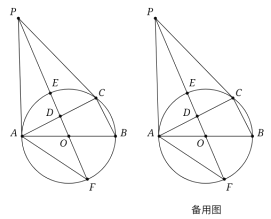
(1)证明:EF2=4ODOP;
(2)若tan∠AFP=![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】
(1)由D是AC中点可得OD⊥AC,则PA=PC;设∠PAD=∠1,∠PCD=∠2,∠BAC=∠3,可得∠1=∠2;又∠2=∠B,AB是直径,则∠ACB=90°,进一步说明∠PAB=90°;再由摄影定理可得:△AOD∽△POA,得![]() 即
即![]() ,再根据AO=
,再根据AO=![]() EF,即可完成证明;
EF,即可完成证明;
(2)由tan∠AFP=![]() ,设AD=2,DF=3,则A0=OF=x,OD=3-x ,AD2+DO2=A02,可求x=
,设AD=2,DF=3,则A0=OF=x,OD=3-x ,AD2+DO2=A02,可求x=![]() ,进一步即可完成解答.
,进一步即可完成解答.
解:(1)∵D是AC中点,
∴OD⊥AC,
∴PA=PC
设∠PAD=∠1,∠PCD=∠2,∠BAC=∠3
∴∠1=∠2,
∵∠2=∠B,AB是直径
∴∠ACB=90°,∠B+∠3=90°
∴∠1+∠3=90°,
∴∠PAB=90°
根据射影定理可得△AOD∽△POA
∴![]() 即
即![]()
∵AO=![]() EF,
EF,
∴EF2=4ODOP;
(2) 由tan∠AFP=![]() ,设AD=2,DF=3,则A0=OF=x,OD=3-x ,
,设AD=2,DF=3,则A0=OF=x,OD=3-x ,
∴AD2+DO2=A02即22+(3-x)2=x2,求得x=![]() ,
,
∴DO=![]()
∵AO=BO,AD=CD,
∴OD=![]() BC,
BC,
∴BC=2DO=![]()
∵DE=OE-OD=![]()
∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴正半轴交于A点,与y轴正半轴交于B,直线AB的解析式为y=﹣x+3.
(1)求抛物线解析式;
(2)P为线段OA上一点(不与O、A重合),过P作PQ⊥x轴交抛物线于Q,连接AQ,M为AQ中点,连接PM,过M作MN⊥PM交直线AB于N,若点P的横坐标为t,点N的横坐标为n,求n与t的函数关系式;
(3)在(2)的条件下,连接QN并延长交y轴于E,连接AE,求t为何值时,MN∥AE.
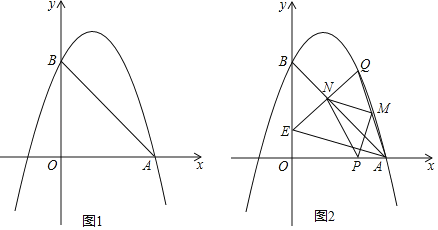
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;
C.仅家长自己参与; D.家长和学生都未参与.

请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了________名学生;
(2)补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN为⊙OD的直径,PM为⊙O的切线,PM=MN=4,点A在⊙O上,AB⊥PA交MN于B.若B为ON的中点,则AB的长为( )
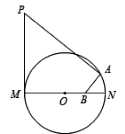
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C = 90°,![]() .D为BC上一点,且到A,B两点的距离相等.
.D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B = 35°,求∠CAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形 ABCD 中,E 是边 BC 边上一点,连接 DE 交对角线 AC 于点 F,若 AB=6,AD=8,BE=2,则 AF 的长为 _________________ ![]()
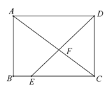
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据规定,我市将垃圾分为了四类:可回收物、易腐垃圾、有害垃圾和其他垃圾四大类. 现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投进两个不同的垃圾桶,投放正确的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com