
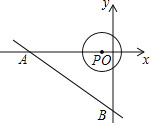
【题目】如图,直线y=-![]() x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是_______.
x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是_______.
【答案】(-![]() ,0)或P(-
,0)或P(-![]() ,0)
,0)
【解析】
根据函数解析式求得A(-4,0),B(0.-3),得到OA=4,OB=3,根据勾股定理得到AB=5,设⊙P与直线AB相切于D,连接PD,则PD⊥AB,PD=1,根据相似三角形的性质即可得到结论.
∵直线y=-![]() x-3交x轴于点A,交y轴于点B,
x-3交x轴于点A,交y轴于点B,
∴令x=0,得y=-3,令y=0,得x=-4,
∴A(-4,0),B(0.-3),
∴OA=4,OB=3,
∴AB=5,
设⊙P与直线AB相切于D,连接PD,
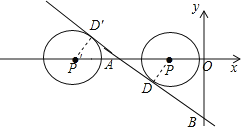
则PD⊥AB,PD=1,
∵∠ADP=∠AOB=90°,∠PAD=∠BAO,
∴△APD∽△ABO,
∴![]() ,
,
∴![]() ,
,
∴AP=![]() ,
,
∴OP=![]() 或OP=
或OP=![]() ,
,
∴P(-![]() ,0)或P(-
,0)或P(-![]() ,0),
,0),
故答案为:(-![]() ,0)或P(-
,0)或P(-![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
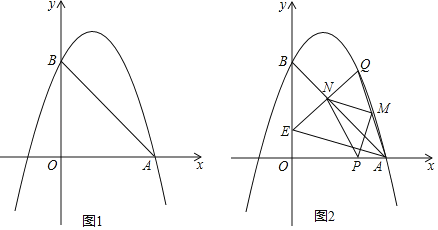
【题目】如图,抛物线y=﹣x2+bx+c与x轴正半轴交于A点,与y轴正半轴交于B,直线AB的解析式为y=﹣x+3.
(1)求抛物线解析式;
(2)P为线段OA上一点(不与O、A重合),过P作PQ⊥x轴交抛物线于Q,连接AQ,M为AQ中点,连接PM,过M作MN⊥PM交直线AB于N,若点P的横坐标为t,点N的横坐标为n,求n与t的函数关系式;
(3)在(2)的条件下,连接QN并延长交y轴于E,连接AE,求t为何值时,MN∥AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
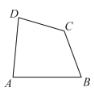
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”,例如:如图,四边形![]() 是“等对角四边形”,
是“等对角四边形”,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
(1)已知:在“等对角四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,求对角线
,求对角线![]() 的长;
的长;
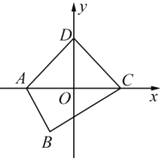
(2)已知:如图,在平面直角坐标系![]() 中,四边形
中,四边形![]() 是“等对角四边形”,其中
是“等对角四边形”,其中![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,抛物线
轴上,抛物线![]() 过点
过点![]() 、
、![]() ,点
,点![]() 在抛物线上,满足
在抛物线上,满足![]() 的
的![]() 点至少有3个时,总有不等式
点至少有3个时,总有不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,点O在坐标原点,已知点A(3,1)、B(2,0)、C(4,﹣2).
(1)求证:△AOB∽△OCB;
(2)求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
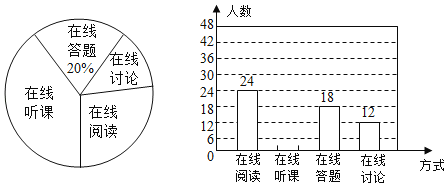
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解决学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调査,并根据调査结果绘制成如下两幅不完整的统计图.请你根据图中提供的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图
(3)若该校共有学生2100人,请你估计该校对在线阅读最感兴趣的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;
C.仅家长自己参与; D.家长和学生都未参与.

请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了________名学生;
(2)补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com