
【题目】如图,已知![]() 和
和![]() 均为等腰三角形,
均为等腰三角形,![]() ,
,![]() ,将这两个三角形放置在一起.
,将这两个三角形放置在一起.
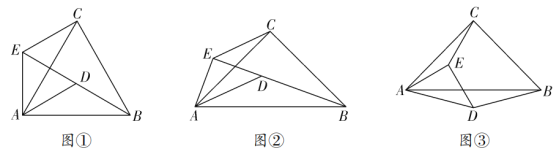
(1)问题发现
如图①,当![]() 时,点
时,点![]() 、
、![]() 、
、![]() 在同一直线上,连接
在同一直线上,连接![]() ,则
,则![]() 的度数为__________,线段
的度数为__________,线段![]() 、
、![]() 、
、![]() 之间的数量关系是__________;
之间的数量关系是__________;
(2)拓展探究
如图②,当![]() 时,点
时,点![]() 、
、![]() 、
、![]() 在同一直线上,连接
在同一直线上,连接![]() .请判断
.请判断![]() 的度数及线段
的度数及线段![]() 、
、![]() 、
、![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)解决问题
如图③,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 、
、![]() ,在
,在![]() 绕点
绕点![]() 旋转的过程中,当
旋转的过程中,当![]() 时,请直接写出
时,请直接写出![]() 的长
的长
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)证明△ACE≌△ABD,得出CE=AD,∠AEC=∠ADB,即可得出结论;(2)证明△ACE∽△ABD,得出∠AEC=∠ADB,![]() ,即可得出结论;(3)先判断出
,即可得出结论;(3)先判断出![]() ,再求出
,再求出![]() ,①当点E在点D上方时,先判断出四边形APDE是矩形,求出AP=DP=AE=2,再根据勾股定理求出,BP=6,得出BD=4;②当点E在点D下方时,同①的方法得,AP=DP=AE=1,BP=4,进而得出BD=BP+DP=8,即可得出结论.
,①当点E在点D上方时,先判断出四边形APDE是矩形,求出AP=DP=AE=2,再根据勾股定理求出,BP=6,得出BD=4;②当点E在点D下方时,同①的方法得,AP=DP=AE=1,BP=4,进而得出BD=BP+DP=8,即可得出结论.
(1)在△ABC为等腰三角形,AC=BC,∠ACB=60°,
∴△ABC是等边三角形,
∴AC=AB,∠CAB=60°,
同理:AE=AD,∠ADE=∠EAD=60°,
∴∠EAD=∠CAB,
∴∠EAC=∠DAB,
∴△ACE≌△ABD(SAS),
∴CE=AD,∠AEC=∠ADB,
∵点B、D、E在同一直线上,
∴∠ADB=180°-∠ADE=120°,
∴∠AEC=120°,
∴![]()
∵DE=AE,
∴BE=DE+BD=AE+CE,
故答案为60°,BE=AE+CE;
(2)![]() .
.
理由如下:![]() 和
和![]() 均为等腰三角形,
均为等腰三角形, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() 点
点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,
![]() ,
,
![]() .
.
![]() ;
;
(3)由(2)知,△ACE∽△ABD,
∴![]() ,
,
在Rt△ABC中,![]() ,
,
∴![]() ;
;
①当点E在点D上方时,如图③,过点A作AP⊥BD交BD的延长线于P,
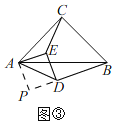
∵DE⊥BD,
∴∠PDE=∠AED=∠APD,
∴四边形APDE是矩形,
∵AE=DE,
∴矩形APDE是正方形,
∴AP=DP=AE=2,
在Rt△APB中,根据勾股定理得, ![]()
∴BD=BP-AP=4,
∴![]() ;
;
②当点E在点D下方时,如图④,
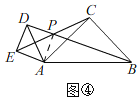
同①的方法得,AP=DP=AE=2,BP=4,
∴BD=BP+DP=8,
∴![]() ,
,
即:CE的长为![]() 或
或![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
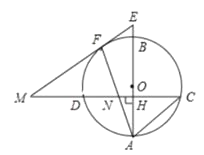
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,在CD上有点N满足CN=CA,AN交圆O于点F,过点F的AC的平行线交CD的延长线于点M,交AB的延长线于点E.
(1)求证:EM是圆O的切线;
(2)若AC:CD=5:8,AN=3![]() ,求圆O的直径长度.
,求圆O的直径长度.
(3)在(2)的条件下,直接写出FN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900D.y=﹣2(x﹣65)2+2000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F .
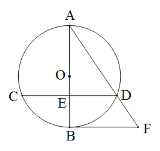
(1)求证:BF是⊙O的切线;
(2)连结BC,若⊙O的半径为2,tan∠BCD=![]() ,求线段AD的长.
,求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 以
以![]() 为直径的⊙
为直径的⊙![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作⊙
作⊙![]() 的切线交
的切线交![]() 于点
于点![]() ,连接
,连接![]() .
.
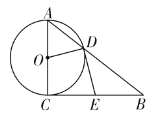
(1)求证:![]() ;
;
(2)连接![]() ,并延长
,并延长![]() 交圆
交圆![]() 于点
于点![]() ,
,![]() .
.
填空:①当![]() __________时,四边形
__________时,四边形![]() 是菱形;
是菱形;
②当![]() 的长=__________时,四边形
的长=__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
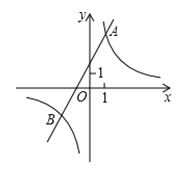
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .
(1)求这两个函数的关系式;
(2)观察图象,直接写出使得y1>y2成立的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新能源汽车的发展,某公交公司将用新能源公交车淘汰某一条线路上“冒黑烟”较严重的燃油公交车,计划购买A型和B型新能源公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需300万元;若购买A型公交车2辆,B型公交车1辆,共需270万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1000万元,且确保这10辆公交车在该线路的年均载客量总和不少于900万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
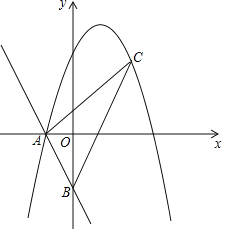
【题目】一次函数y=﹣2x﹣2分别与x轴、y轴交于点A、B.顶点为(1,4)的抛物线经过点A.
(1)求抛物线的解析式;
(2)点C为第一象限抛物线上一动点.设点C的横坐标为m,△ABC的面积为S.当m为何值时,S的值最大,并求S的最大值;
(3)在(2)的结论下,若点M在y轴上,△ACM为直角三角形,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com