
【题目】已知:如图,⊙O的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F .
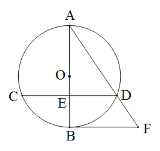
(1)求证:BF是⊙O的切线;
(2)连结BC,若⊙O的半径为2,tan∠BCD=![]() ,求线段AD的长.
,求线段AD的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由垂径定理可证AB⊥CD,由CD∥BF,得AB⊥BF,则BF是⊙O的切线;
(2)连接BD,根据同弧所对圆周角相等得到∠BCD =∠BAD,再利用圆的性质得到∠ADB=90°, tan∠BCD= tan∠BAD=![]() ,得到BD与AD的关系,再利用解直角三角形可以得到BD、AD与半径的关系,进一步求解即可得到答案.
,得到BD与AD的关系,再利用解直角三角形可以得到BD、AD与半径的关系,进一步求解即可得到答案.
(1)证明:∵ ⊙O的直径AB与弦CD相交于点E,且E为CD中点
∴ AB ⊥CD, ∠AED =90°
∵ CD // BF
∴ ∠ABF =∠AED =90°
∴ AB⊥BF
∵ AB是⊙O的直径
∴ BF是⊙O的切线
(2)解:连接BD
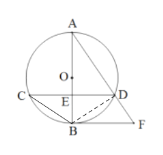
∵∠BCD、∠BAD是同弧所对圆周角
∴∠BCD =∠BAD
∵ AB是⊙O的直径
∴∠ADB=90°
∵ tan∠BCD= tan∠BAD=![]()
∴![]()
∴设BD=3x,AD=4x
∴AB=5x
∵ ⊙O的半径为2,AB=4
∴5x=4,x=![]()
∴AD=4x=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P和点![]() 关于x轴对称,点
关于x轴对称,点![]() 和点
和点![]() 关于直线l对称,则称点
关于直线l对称,则称点![]() 是点P关于x轴,直线l的二次对称点.
是点P关于x轴,直线l的二次对称点.
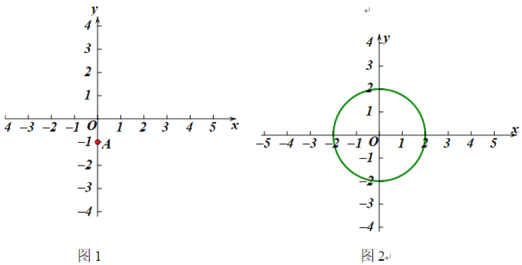
(1)如图1,点A(0,-1).
①若点B是点A关于x轴,直线![]() :x=2的二次对称点,则点B的坐标为 ;
:x=2的二次对称点,则点B的坐标为 ;
②点C (-4,1)是点A关于x轴,直线![]() :x=a的二次对称点,则a的值为 ;
:x=a的二次对称点,则a的值为 ;
③点D(-1,0)是点A关于x轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为 ;
的表达式为 ;
(2)如图2,O的半径为2.若O上存在点M,使得点M′是点M关于x轴,直线![]() :x = b的二次对称点,且点M′在射线
:x = b的二次对称点,且点M′在射线![]() (x≥0)上,b的取值范围是 ;
(x≥0)上,b的取值范围是 ;
(3)E(0,t)是y轴上的动点,E的半径为2,若E上存在点N,使得点N′是点N关于x轴,直线![]() :
:![]() 的二次对称点,且点N′在x轴上,求t的取值范围.
的二次对称点,且点N′在x轴上,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台![]() 型电脑和
型电脑和![]() 型打印机.如果购买1台
型打印机.如果购买1台![]() 型电脑,2台
型电脑,2台![]() 型打印机,一共需要花费6200元;如果购买2台
型打印机,一共需要花费6200元;如果购买2台![]() 型电脑,1台
型电脑,1台![]() 型打印机,一共需要花费7900元.
型打印机,一共需要花费7900元.
(1)求每台![]() 型电脑和每台
型电脑和每台![]() 型打印机的价格分别是多少元?
型打印机的价格分别是多少元?
(2)如果学校购买![]() 型电脑和
型电脑和![]() 型打印机的预算费用不超过20000元,并且购买
型打印机的预算费用不超过20000元,并且购买![]() 型打印机的台数要比购买
型打印机的台数要比购买![]() 型电脑的台数多1台,那么该学校至多能购买多少台
型电脑的台数多1台,那么该学校至多能购买多少台![]() 型打印机?
型打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一农户要建一个矩形鸡舍,鸡舍的一边利用长为a米的墙,另外三边用25米长的篱笆围成,为方便进出,在垂直于墙的一边CD上留一个1米宽的门,
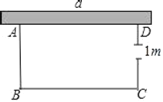
(1)若a=12,问矩形的边长分别为多少时,鸡舍面积为80米2.
(2)问a的值在什么范围时,(1)中的解有两个?一个?无解?
(3)若住房墙的长度足够长,问鸡舍面积能否达到90平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象经过
的图象经过![]() 、
、![]() 、
、![]() 三点.
三点.
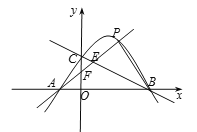
(1)求该二次函数的解析式;
(2)若点M是该二次函数图象上的一点,且满足![]() ,求点M的坐标;
,求点M的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 和
和![]() 均为等腰三角形,
均为等腰三角形,![]() ,
,![]() ,将这两个三角形放置在一起.
,将这两个三角形放置在一起.
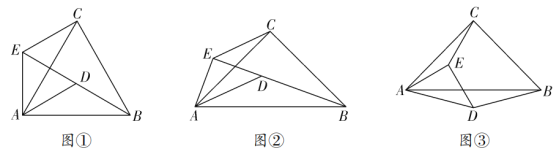
(1)问题发现
如图①,当![]() 时,点
时,点![]() 、
、![]() 、
、![]() 在同一直线上,连接
在同一直线上,连接![]() ,则
,则![]() 的度数为__________,线段
的度数为__________,线段![]() 、
、![]() 、
、![]() 之间的数量关系是__________;
之间的数量关系是__________;
(2)拓展探究
如图②,当![]() 时,点
时,点![]() 、
、![]() 、
、![]() 在同一直线上,连接
在同一直线上,连接![]() .请判断
.请判断![]() 的度数及线段
的度数及线段![]() 、
、![]() 、
、![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)解决问题
如图③,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 、
、![]() ,在
,在![]() 绕点
绕点![]() 旋转的过程中,当
旋转的过程中,当![]() 时,请直接写出
时,请直接写出![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
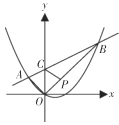
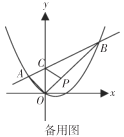
【题目】如图,在平面直角坐标系中,抛物线![]() 上有两点
上有两点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 到两坐标轴的距离相等.点
到两坐标轴的距离相等.点![]() 到两坐标轴的距离也相等.
到两坐标轴的距离也相等.
(1)求点![]() ,
,![]() 的坐标并直接写出
的坐标并直接写出![]() 的形状;
的形状;
(2)若点![]() 为线段
为线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,当
,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上一动点,当
轴上一动点,当![]() 是以
是以![]() 为斜边的直角三角形时,求点
为斜边的直角三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与
的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与![]() 交于点F,延长BA到点G,使得
交于点F,延长BA到点G,使得![]() ,连接FG.
,连接FG.
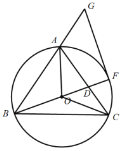
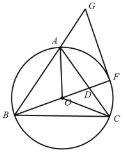
备用图
(1)求证:FG是![]() 的切线;
的切线;
(2)若![]() 的半径为4.
的半径为4.
①当![]() ,求AD的长度;
,求AD的长度;
②当![]() 是直角三角形时,求
是直角三角形时,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com