
【题目】如图,有一农户要建一个矩形鸡舍,鸡舍的一边利用长为a米的墙,另外三边用25米长的篱笆围成,为方便进出,在垂直于墙的一边CD上留一个1米宽的门,
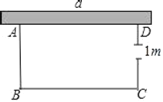
(1)若a=12,问矩形的边长分别为多少时,鸡舍面积为80米2.
(2)问a的值在什么范围时,(1)中的解有两个?一个?无解?
(3)若住房墙的长度足够长,问鸡舍面积能否达到90平方米?
【答案】(1)矩形鸡舍的长为10m,宽为8m;(2)当a≥16时,(1)中的解有两个,当10≤a<16时,(1)中的解有一个,当0<a<10时,无解;(3)所围成鸡舍面积不能为90平方米.
【解析】
(1)设长为xm,根据所用篱笆长为25m得宽为26-2x, 再由x(26﹣2x)=80解出x的值,再判断其小于12则符合.
(2)根据(1)知,以靠墙的边长为10或16米为临界点可分为三个范围分别是a≥16,解有两个,10≤a<16,解有一个,0<a<10无解.
(3)根据(1)中的一元二次方程,判断其根的判别式是否大于等于0即可.
(1)设矩形鸡舍垂直于房墙的一边长为xm,则矩形鸡舍的另一边长为(26﹣2x)m.
依题意,得x(26﹣2x)=80,
解得x1=5,x2=8.
当x=5时,26﹣2x=16>12(舍去),
当x=8时,26﹣2x=10<12.
答:矩形鸡舍的长为10m,宽为8m.
(2)由(1)知,靠墙的边长为10或16米,
∴当a≥16时,(1)中的解有两个,
当10≤a<16时,(1)中的解有一个,
当0<a<10时,无解.
(3)当S=90m2,
则x(26﹣2x)=90,
整理得:x2﹣13x+45=0,
则△=b2﹣4ac=169﹣180=﹣11<0,
故所围成鸡舍面积不能为90平方米.
答:所围成鸡舍面积不能为90平方米.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°.BE平分∠ABC交AC于点D,交△ABC的外接圆于点E,过点E作EF⊥BC交BC的延长线于点F.请补全图形后完成下面的问题:
(1)求证:EF是△ABC外接圆的切线;
(2)若BC=5,sin∠ABC=![]() ,求EF的长.
,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
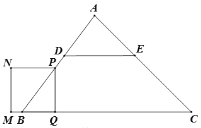
【题目】如图,在△ABC中, tan∠ABC=![]() ,∠C=45°,点D、E分别是边AB、AC上的点,且DE∥BC,BD=DE=5,动点P从点B出发,沿B-D-E-C向终点C运动,在BD-DE上以每秒5个单位长度的速度运动,在EC上以每秒
,∠C=45°,点D、E分别是边AB、AC上的点,且DE∥BC,BD=DE=5,动点P从点B出发,沿B-D-E-C向终点C运动,在BD-DE上以每秒5个单位长度的速度运动,在EC上以每秒![]() 个单位长度的速度运动,过点P作PQ⊥BC于点Q,以PQ为边作正方形PQMN,使点B、点N始终在PQ同侧. 设点P的运动时间为
个单位长度的速度运动,过点P作PQ⊥BC于点Q,以PQ为边作正方形PQMN,使点B、点N始终在PQ同侧. 设点P的运动时间为![]() (
(![]() )(
)(![]() >0),正方形PQMN与△ABC重叠部分图形的面积为S.
>0),正方形PQMN与△ABC重叠部分图形的面积为S.
(1)当点P在BD-DE上运动时,用含![]() 的代数式表示线段DP的长.
的代数式表示线段DP的长.
(2)当点N落在AB边上时,求![]() 的值.
的值.
(3)当点P在DE上运动时,求S与![]() 之间的函数关系式.
之间的函数关系式.
(4)当点P出发时,有一点H从点D出发,在线段DE上以每秒5个单位长度的速度沿D-E-D连续做往返运动,直至点P停止运动时,点H也停止运动.连结HN,直接写出HN与DE所夹锐角为45°时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900D.y=﹣2(x﹣65)2+2000
查看答案和解析>>
科目:初中数学 来源: 题型:
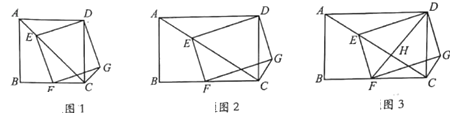
【题目】在矩形ABCD中,AB=a,AD=b,点E为对角线AC上一点,连接DE,以DE为边,作矩形DEFG,点F在边BC上;
(1)观察猜想:如图1,当a=b时,![]() =______,∠ACG=______;
=______,∠ACG=______;
(2)类比探究:如图2,当a≠b时,求![]() 的值(用含a、b的式子表示)及∠ACG的度数;
的值(用含a、b的式子表示)及∠ACG的度数;
(3)拓展应用:如图3,当a=6,b=8,且DF⊥AC,垂足为H,求CG的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F .
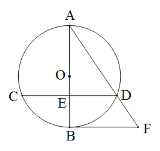
(1)求证:BF是⊙O的切线;
(2)连结BC,若⊙O的半径为2,tan∠BCD=![]() ,求线段AD的长.
,求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 以
以![]() 为直径的⊙
为直径的⊙![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作⊙
作⊙![]() 的切线交
的切线交![]() 于点
于点![]() ,连接
,连接![]() .
.
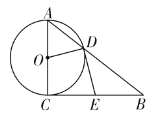
(1)求证:![]() ;
;
(2)连接![]() ,并延长
,并延长![]() 交圆
交圆![]() 于点
于点![]() ,
,![]() .
.
填空:①当![]() __________时,四边形
__________时,四边形![]() 是菱形;
是菱形;
②当![]() 的长=__________时,四边形
的长=__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
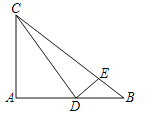
【题目】在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB边上一动点(点D与点A、B不重合),联结CD,过点D作DE⊥DC交边BC于点E.
(1)如图,当ED=EB时,求AD的长;
(2)设AD=x,BE=y,求y关于x的函数解析式并写出函数定义域;
(3)把△BCD沿直线CD翻折得△CDB',联结AB',当△CAB'是等腰三角形时,直接写出AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com