
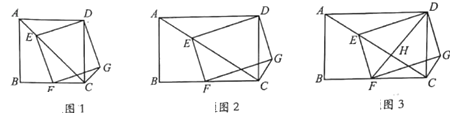
【题目】在矩形ABCD中,AB=a,AD=b,点E为对角线AC上一点,连接DE,以DE为边,作矩形DEFG,点F在边BC上;
(1)观察猜想:如图1,当a=b时,![]() =______,∠ACG=______;
=______,∠ACG=______;
(2)类比探究:如图2,当a≠b时,求![]() 的值(用含a、b的式子表示)及∠ACG的度数;
的值(用含a、b的式子表示)及∠ACG的度数;
(3)拓展应用:如图3,当a=6,b=8,且DF⊥AC,垂足为H,求CG的长;
【答案】(1)1,90°;(2)∠ACG =90°,![]() ;(3)CG=
;(3)CG=![]() .
.
【解析】
(1)利用SAS可证![]() ,由全等三角形的性质知
,由全等三角形的性质知![]() ,所以
,所以![]() ,结合
,结合![]() 可得
可得![]() ;
;
(2)方法一:过点E作EM⊥BC,EN⊥DC,垂足分别为M和N,连接EG,FD交于点O,连接OC,利用矩形的性质及三角形内角和定理可得∠ACG =90°,可证△DAE∽△DCG,由相似三角形的对应线段成比例可得![]() 的值;方法二:结合垂直与矩形的性质由两组对应角分别相等的两个三角形相似可得△CEN∽△CAD,△END∽△EMF,由相似三角形的性质可得
的值;方法二:结合垂直与矩形的性质由两组对应角分别相等的两个三角形相似可得△CEN∽△CAD,△END∽△EMF,由相似三角形的性质可得![]() ,
,![]() ,由两组对应线段成比例及其夹角相等的两个三角形相似可得△ADE∽△CDG,根据其性质可得结论;
,由两组对应线段成比例及其夹角相等的两个三角形相似可得△ADE∽△CDG,根据其性质可得结论;
(3)由勾股定理得AC长,由相似三角形的判定可得△ CDH∽△CAD,△DEF∽△ADC,由相似三角形的性质可得CH的长及∠EDH=∠CAD,利用AAS得 △DHE≌△DHC,根据全等的性质可得EH的长,进一步可知AE长,结合![]() 即知CG的值.
即知CG的值.
解:(1)![]() 根据题意,易知矩形ABCD与矩形DEFG为正方形
根据题意,易知矩形ABCD与矩形DEFG为正方形
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2)方法一:连接EG,FD交于点O,连接OC.
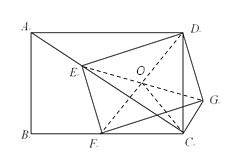
∵四边形EDGF和ABCD是矩形
∴∠ADC=∠EDG=90°
即∠ADE+∠EDC=∠CDG+∠EDC
∴∠ADE =∠CDG
∵∠ BCD=90°OF=OD
∴OC=img src="http://thumb.zyjl.cn/Upload/2020/11/27/12/c71d404d/SYS202011271221588355837411_DA/SYS202011271221588355837411_DA.021.png" width="41" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />
在矩形DEFG中,EG=DF ∴ OC=![]()
∵OE=OG![]() ∴OE=OC=OG
∴OE=OC=OG
∴∠OEC=∠OCE ∠OCF=∠OFC
又∵∠OEC+∠ECG+∠EGC=180°
∴2∠OCE+2∠OCG =180°
∴∠OCE+∠OCG =90°即∠ACG =90°
∴∠ECD+∠DCG =90°
在Rt△ADC中,∠ECD+∠DAC =90°∴∠DAE=∠DCG
∴△DAE∽△DCG
∴![]()
方法二:过点E作EM⊥BC,EN⊥DC,垂足分别为M和N.
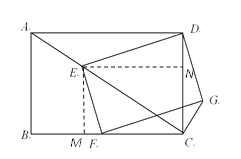
∵∠EMC=∠MCN=∠ENC=90°
∴四边形EMCN是矩形
∴EM=NC,∠MEN=90°.
∵∠ ENC =∠ADC=90°∴EN∥AD
∴△CEN∽△CAD
∴![]() 即
即![]()
∵∠MEN=90°∠FED=90°
∴∠MEF=∠NED
又∵∠END =∠EMF =90°
∴△END∽△EMF
∴![]()
又∵EF=DG∴![]()
∵∠ADC=∠EDG=90°
∴△ADE∽△CDG
∴![]() , ∠DAE=∠DCG
, ∠DAE=∠DCG
∵在Rt△ADC中∠DAC+∠ACD=90°
∴∠ACG=∠DCG+∠ACD=90°
(3) ∵AD=8,DC=6 ∴AC=![]() =10
=10
∵DF⊥AC∴![]() ,∠CDH +∠ACD=90°
,∠CDH +∠ACD=90°
∵∠DAC+∠ACD=90°
∴∠CDH=∠DAC
![]()
∴△ CDH∽△CAD
∴CD2=CH·CA ,∠CDH=∠CAD
∵CD=6,AC=10
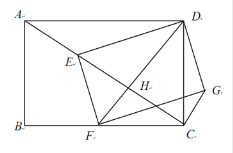
∴CH=![]()
![]()
∵ 由(2)知![]() ∠DEF =∠ADC =90°
∠DEF =∠ADC =90°
∴△DEF∽△ADC
∴∠EDH=∠CAD
∴∠CDH=∠EDH
∵∠DHE=∠DHC=90°DH=DH
∴△DHE≌△DHC
∴EH=CH=![]()
∴AE=AC-EH-HC=![]()
∵![]() ∴CG=
∴CG=![]()


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
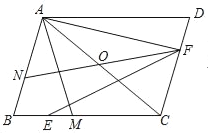
【题目】如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.
(1)若BM=4,MC=3,AC=![]() ,求AM的长度;
,求AM的长度;
(2)若∠ACB=45°,求证:AN+AF=![]() EF.
EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
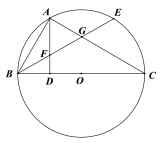
【题目】如图,BC是⊙O的直径,点A在⊙上,AD⊥BC,垂足为D,![]() ,BE分别交AD、AC与点F、G.
,BE分别交AD、AC与点F、G.
(1)证明:FA=FB.
(2)BD=DO=2,求弧EC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)两种机器人每小时分别分类多少垃圾?
(2)现在两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
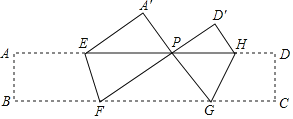
【题目】如图,把矩形ABCD沿EF,GH折叠,使点B,C落在AD上同一点P处,∠FPG=90°,△A′EP的面积是8![]() ,△D′PH的面积是4
,△D′PH的面积是4![]() ,则矩形ABCD的面积等于_____.
,则矩形ABCD的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一农户要建一个矩形鸡舍,鸡舍的一边利用长为a米的墙,另外三边用25米长的篱笆围成,为方便进出,在垂直于墙的一边CD上留一个1米宽的门,
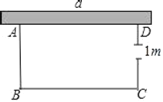
(1)若a=12,问矩形的边长分别为多少时,鸡舍面积为80米2.
(2)问a的值在什么范围时,(1)中的解有两个?一个?无解?
(3)若住房墙的长度足够长,问鸡舍面积能否达到90平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
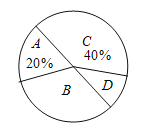
【题目】对某校学生寒假阅读时间情况调查,抽样统计绘制了两幅不完整的统计图,请结合信息解决下列问题:
阅读时间(小时) |
|
|
|
|
人数 | 60 | 80 |
(1)这次统计A类 人;D类 人;
(2)如果该校有1200学生,那么D类学生数量约为多少人?
(3)甲、乙、丙、丁4名学生是阅读属于D类学生,他们分别来自九年级1人,八年级1人,七年级2人,现抽取2人电话回访,则抽取到2人同为七年级学生的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小高发现电线杆 AB 的影子落在土坡的坡面CD和地面 BC上,量得 CD= 12 米 , BC= 20 米 ,CD与地面成30°角,且此时测得1米杆的影长为2 米,求电线杆的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等且有一组对角互补的凸四边形叫做等补四边形
(1)概念理解
①根据上述定义举一个等补四边形的例子:
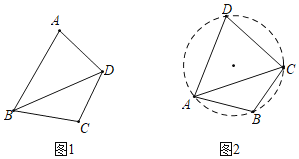
②如图1,四边形ABCD中,对角线BD平分∠ABC,∠A+∠C=180°,求证:四边形ABCD是等补四边形
(2)性质探究:
③小明在探究时发现,由于等补四边形有一组对角互补,可得等补四边形的四个顶点共圆,如图2,等补四边形ABCD内接于⊙O,AB=AD,则∠ACD ∠ACB(填“>”“<”或“=“);
④若将两条相等的邻边叫做等补四边形的“等边”,等边所夹的角叫做“等边角”,它所对的角叫做“等边补角”连接它们顶点的对角线叫做“等补对角线”,请用语言表述③中结论:
(3)问题解决
在等补四边形ABCD中,AB=BC=2,等边角∠ABC=120°,等补对角线BD与等边垂直,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com