
【题目】如图,已知二次函数![]() 的图象经过
的图象经过![]() 、
、![]() 、
、![]() 三点.
三点.
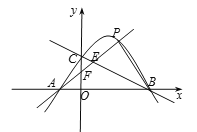
(1)求该二次函数的解析式;
(2)若点M是该二次函数图象上的一点,且满足![]() ,求点M的坐标;
,求点M的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]()
(2)![]() 或(-5,-18)
或(-5,-18)
(3)![]()
【解析】
(1)已知三点坐标,代入二次函数解析式,得三元一次方程组,可求得二次函数解析式.
(2)已知二次函数解析式,可求得B点坐标为(4,0)当点M在x轴上方时,过C作CM∥AB交抛物线于点M,四边形ABMC为等腰梯形,可求得满足条件的M点坐标.如果M点在x轴下方,先求出直线AC和直线BM的解析式,直线BM的解析式和抛物线的交点即为M点,联立方程求解.
(3)过点P作PH∥y轴交直线BC于点H,可设出P点坐标,从而可表示出PH的长,可表示出△PEB的面积,进一步可表示出直线AP的解析式,可求得F点的坐标,联立直线BC和PA的解析式,可表示出E点横坐标,从而可表示出△CEF的面积,再利用二次函数的性质可求得S2-S1的最小值.
(1)已知二次函数![]() 的图象经过
的图象经过![]() 、
、![]() 、
、![]() 三点
三点
则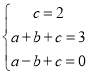
得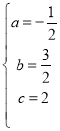
二次函数解析式为:![]()
(2)当点M在x轴上方时,过C作CM∥AB交抛物线于点M,如图1
∵A、B关于对称轴对称,CM关于对称轴对称
∴四边形ABMC为等腰梯形
∴∠CAO=∠MBA,即点M满足条件
∴M(3,2)
当点M在x轴下方时
∵∠MBA=∠CAO
∴BM∥AC
∵C(0,2),
∴可设直线AC解析式为y=kx+2,把A(1,0)代入可求得k=2,
∴直线AC解析式为y=2x+2,
∴可设直线BM解析式为y=2x+m,把B(4,0)代入可求得m=8,
∴直线BM解析式为y=2x8,
联立直线BM和抛物线解析式可得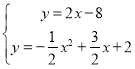 解得
解得![]() 或
或![]()
∴M(5,18)
综上可知满足条件的点M的坐标为(3,2)或(5,18);
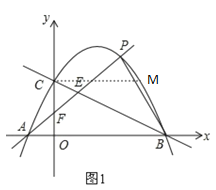
(3)
过点P作PH∥y轴交直线BC于点H,如图2,
设![]()
由B、C两点的坐标可求得直线BC的解析式为y=![]() x+2
x+2
∴H(t,![]() t+2)
t+2)
∴PH=yPyH=![]() (
(![]() t+2)=
t+2)=![]()
设直线AP的解析式为y=px+q
∴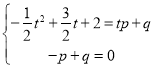
解得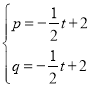
∴直线AP的解析式为![]() ,令x=0可得
,令x=0可得![]()
∴F(0,![]() ),
),
∴CF=2(![]() )=
)=![]()
联立直线AP和直线BC解析式可得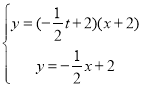
解得x=![]() ,即E点的横坐标为
,即E点的横坐标为![]()
![]()
![]()
![]()
![]()
![]()
当![]() 时,S2-S1的最小值为-
时,S2-S1的最小值为-![]()



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
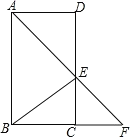
【题目】如图,在ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;(2)若AB=14,DE=8,求sin∠AEB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在二次函数的图象中,小明同学观察得出了下面几条信息:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤关于
;⑤关于![]() 的一元二次方程
的一元二次方程![]() 无实数根,其中信息正确的个数为( ).
无实数根,其中信息正确的个数为( ).
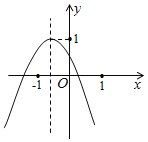
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F .
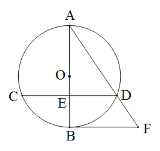
(1)求证:BF是⊙O的切线;
(2)连结BC,若⊙O的半径为2,tan∠BCD=![]() ,求线段AD的长.
,求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了积极助力脱贫攻坚工作,如期打赢脱贫攻坚战,某驻村干部带领村民种植草莓,在每年成熟期都会吸引很多人到果园去采摘.现有甲、乙两家果园可供采摘,这两家草莓的品质相同,售价均为每千克30元,但是两家果园的采摘方案不同:
甲果园:每人需购买20元的门票一张,采摘的草莓按6折优惠;
乙果园:不需要购买门票,采摘的草莓按售价付款不优惠.
设小明和爸爸妈妈三个人采摘的草莓数量为![]() 千克,在甲、乙果园采摘所需总费用分别为
千克,在甲、乙果园采摘所需总费用分别为![]() 、
、![]() 元,其函数图象如图所示.
元,其函数图象如图所示.

(1)分别写出![]() 、
、![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)请求出图中点![]() 的坐标;
的坐标;
(3)请根据函数图象,直接写出小明一家选择哪家果园采摘更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
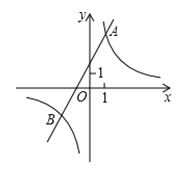
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .
(1)求这两个函数的关系式;
(2)观察图象,直接写出使得y1>y2成立的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
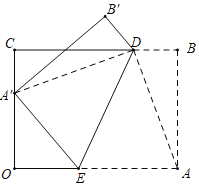
【题目】如图,长方形OABC中,OA=8,AB=6,点D在边BC上,且CD=3DB,点E是边OA上一点,连接DE,将四边形ABDE沿DE折叠,若点A的对称点A′恰好落在边OC上,则OE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com