练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

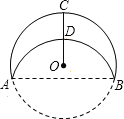
    【题目】如图，将半径为8的⊙O折叠，弧AB恰好经过与AB垂直的半径OC的中点D，则折痕AB的长___________ .

    【答案】

    【解析】

    延长CO交AB于E点，交⊙O于点F，连接OB，由OC与AB垂直，根据垂径定理得到E为AB的中点，然后利用D是OC的中点和对称即可求出OD、CD、DE的长，从而求出OE，然后由OB，OE的长，根据勾股定理求出AE的长，进而得出AB的长．

    解：延长CO交AB于E点，交⊙O于点F，连接OB，

    ∵CE⊥AB，

    ∴E为AB的中点，

    ∵D是OC的中点，OC=8

    ∴CD=4，OD=4，OB=8，CF=2OC=16

    根据对称的性质可得：

    DE=DF=（CF－CD）=6

    OE=DE－OD=2

    在Rt△OEB中，根据勾股定理可得：

    ∴AB=

    故答案为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，一艘海轮位于灯塔P的南偏东30°方向，距离灯塔100海里的A处，它计划沿正北方向航行，去往位于灯塔P的北偏东45°方向上的B处．

    （1）问B处距离灯塔P有多远？（结果精确到0.1海里）

    （2）假设有一圆形暗礁区域，它的圆心位于射线PB上，距离灯塔150海里的点O处．圆形暗礁区域的半径为60海里，进入这个区域，就有触礁的危险．请判断海轮到达B处是否有触礁的危险？如果海轮从B处继续向正北方向航行，是否有触礁的危险？并说明理由．（参考数据：≈1.414，≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

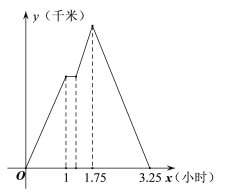
    【题目】已知A地，火神山医院、B地顺次在一条笔直的公路上，且A地、B地距火神山医院的路程相同，甲、乙两家车队分别从A、B两地向火神山医院运送货物，甲车队比乙车队晚出发0.75小时． 为避免拥堵，总调度部门通知距火神山医院更近的车队进工地卸货（卸货时间忽略不计），然后原路原速返回，而另一车队则在火神山医院40千米处等待直到另一车队卸货完毕后再按原速继续行驶进入工地，卸货后原路原速返回． 甲车队距A地的路程（千米）与甲车队行驶的时间（小时）之间的函数关系如图所示：

    （1）甲车队的速度为 千米/时，乙车队的速度为 千米/时，A地与火神山医院之间的距离为 千米．

    （2）甲车队原路返回时与之间的函数关系式．

    （3）直接写出两车队相距80千米时的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

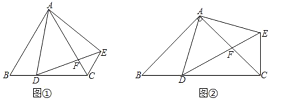
    【题目】如图①，在中，，，为边上一点（不与点，重合），将线段绕点逆时针旋转得到，连接，则：

    （1）①的度数是 ；②线段，，之间的数量关系是 ；

    （2）如图②，在中，，，为边上一点（不与点，重合），将线段绕点逆时针旋转得到，连接，请判断线段，，之间的数量关系，并说明理由；

    （3）如图②，与交于点，在（2）条件下，若，求的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校准备购买若干台型电脑和型打印机.如果购买1台型电脑，2台型打印机，一共需要花费6200元；如果购买2台型电脑，1台型打印机，一共需要花费7900元．

    （1）求每台型电脑和每台型打印机的价格分别是多少元？

    （2）如果学校购买型电脑和型打印机的预算费用不超过20000元，并且购买型打印机的台数要比购买型电脑的台数多1台，那么该学校至多能购买多少台型打印机？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

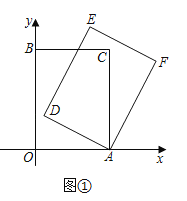
    【题目】在平面直角坐标系中，四边形是矩形，点，点，点．以点为中心，顺时针旋转矩形，得到矩形，点的对应点分别为，记旋转角为．

    (1)如图①，当时，求点的坐标；

    (2)如图②，当点落在的延长线上时，求点的坐标；

    (3)当点落在线段上时，求点的坐标（直接写出结果即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数的图象经过、、三点．

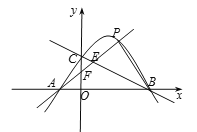
    （1）求该二次函数的解析式；

    （2）若点M是该二次函数图象上的一点，且满足，求点M的坐标；

    （3）点P是该二次函数图象上位于一象限上的一动点，连接PA分别交BC，y轴与点E、F，若、的面积分别为、，求的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一服装批发店出售某品牌童装，每件进价120元，批发价200元，多买优惠；凡是一次买10件以上的，每多买一件，所买的全部服装每件就降低1元，但是最低价为为每件160元，

    （1）求一次至少买多少件，才能以最低价购买？

    （2）写出服装店一次销售x件时，获利润y（元）与x（件）之间的函数关系式，并写出自变量x的取值范围；

    （3）一天，甲批发了46件，乙批发了50件，店主却发现卖46件赚的钱反而比卖50件赚的钱多，你能用数学知识解释这一现象吗？为了不出现这种现象，在其他优惠条件不变的情况下，店家应把最低价每件160元至少提高到多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知和，点在边上，，边与相交于点．

    （1）求证：；

    （2）如果，求证：．

    查看答案和解析>>

    同步练习册答案