
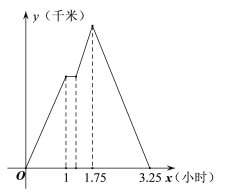
【题目】已知A地,火神山医院、B地顺次在一条笔直的公路上,且A地、B地距火神山医院的路程相同,甲、乙两家车队分别从A、B两地向火神山医院运送货物,甲车队比乙车队晚出发0.75小时. 为避免拥堵,总调度部门通知距火神山医院更近的车队进工地卸货(卸货时间忽略不计),然后原路原速返回,而另一车队则在火神山医院40千米处等待直到另一车队卸货完毕后再按原速继续行驶进入工地,卸货后原路原速返回. 甲车队距A地的路程![]() (千米)与甲车队行驶的时间
(千米)与甲车队行驶的时间![]() (小时)之间的函数关系如图所示:
(小时)之间的函数关系如图所示:
(1)甲车队的速度为 千米/时,乙车队的速度为 千米/时,A地与火神山医院之间的距离为 千米.
(2)甲车队原路返回时![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)直接写出两车队相距80千米时![]() 的值.
的值.
【答案】(1) 80,![]() ,120;(2)
,120;(2)![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
(1)文字信息与图象相结合,有甲车队距火神山医院40千米时,乙车队到达火神山医院卸货.甲车队卸货后返回A地用时1.5小时.据此列方程解答即可;
(2)运用待定系数法解答,即可求出关系式;
(3)根据题意可分为两种情况,在乙车队没有到达火神山医院前和在甲车队卸货结束后,分别列方程解答即可.
解:(1)设甲车队速度为![]() 千米/时,
千米/时,
![]() ,
,
∴![]() ,
,
∴![]() 千米.
千米.
∴ ![]() 千米/时.
千米/时.
故答案为:80,![]() ,120;
,120;
(2)设返回时一次函数为![]() .
.
有![]() ,
,
解得:![]() ,
,![]() ,
,
∴ ![]() .
.
(3)在乙车队没有到达火神山医院前,有
![]() ,
,
解得:![]() ;
;
在甲车队卸货结束后,有
![]() ,
,
解得:![]() ;
;
∴两车队相距80千米时x的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
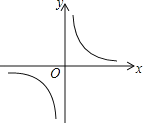
【题目】反比例函数y=![]() 的图象如图所示,以下结论:①常数m<﹣1;②在每个象限内,y随x的增大而增大;③若点A(﹣1,h),B(2,k)在图象上,则h<k;④若点P(x,y)在上,则点P′(﹣x,﹣y)也在图象.其中正确结论的个数是( )
的图象如图所示,以下结论:①常数m<﹣1;②在每个象限内,y随x的增大而增大;③若点A(﹣1,h),B(2,k)在图象上,则h<k;④若点P(x,y)在上,则点P′(﹣x,﹣y)也在图象.其中正确结论的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
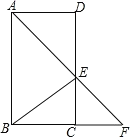
【题目】如图,在ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;(2)若AB=14,DE=8,求sin∠AEB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组根据学习函数的经验,通过列表、描点、连线的方法对函数 y=![]() 的图象与性质进行了研究,研究过程如下,请补充完整.
的图象与性质进行了研究,研究过程如下,请补充完整.
(1)y 与 x 的几组对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 1 | 2 | 3 | … |
y | … |
|
| 6 | 6 | m |
| … |
函数 y=![]() 的自变量 x 的取值范围是 ,m 的值为 ;
的自变量 x 的取值范围是 ,m 的值为 ;
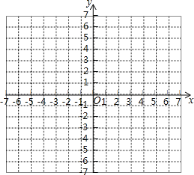
(2)在给出的平面直角坐标系中,描出以上表中各组对应值为坐标的点,画出函数 y=![]() 的大致图象,并写出该函数的两条性质;
的大致图象,并写出该函数的两条性质;
(3)在同一坐标系中画出函数 y1=![]() x 的图象,并根据图象直接写出当 y>y1 时,自变量 x 的取值范围.
x 的图象,并根据图象直接写出当 y>y1 时,自变量 x 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳国际马拉松赛事设有A“全程马拉松”,B“半程马拉松”,C“嘉年华马拉松”三个项目,小智和小慧参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
(1)小智被分配到A“全程马拉松”项目组的概率为 .
(2)用树状图或列表法求小智和小慧被分到同一个项目标组进行志愿服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
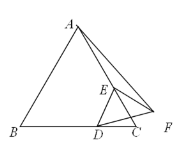
【题目】如图,△ABC是等边三角形,AB=3,E在AC上且AE=![]() AC,D是直线BC上一动点,线段ED绕点E逆时针旋转900,得到线段EF,当点D运动时,则线段AF的最小值是_______
AC,D是直线BC上一动点,线段ED绕点E逆时针旋转900,得到线段EF,当点D运动时,则线段AF的最小值是_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在二次函数的图象中,小明同学观察得出了下面几条信息:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤关于
;⑤关于![]() 的一元二次方程
的一元二次方程![]() 无实数根,其中信息正确的个数为( ).
无实数根,其中信息正确的个数为( ).
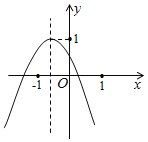
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com