
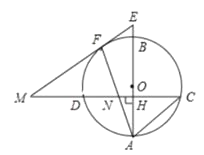
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,在CD上有点N满足CN=CA,AN交圆O于点F,过点F的AC的平行线交CD的延长线于点M,交AB的延长线于点E.
(1)求证:EM是圆O的切线;
(2)若AC:CD=5:8,AN=3![]() ,求圆O的直径长度.
,求圆O的直径长度.
(3)在(2)的条件下,直接写出FN的长度.
【答案】(1)证明见解析;(2)25;(3)![]()
【解析】
(1)连接FO,根据等边对等角可得∠CAN=∠CNA,利用两直线平行内错角相等,可得 ∠CAN=∠MFN ,从而可得∠MFN=∠FNM=∠CAN,利用直角定义可得∠MFO=90°,即证直线ME与圆O相切.
(2)根据垂径定理可得CH=DH=4a , AH=3a.利用勾股定理可得AN的值,从而求出a=3,即得 AH、CH的值 .
设圆的半径为r,则OH=r﹣9,在Rt△OCH中,利用勾股定理可得 ![]() , 解出r值,即得直径.
, 解出r值,即得直径.
(3)连接BF,可证△ANH∽△ABF,可得![]() , 代入数据可求出AF=
, 代入数据可求出AF=![]() , 由FN=AF-AN,即得AN的长度.
, 由FN=AF-AN,即得AN的长度.
(1)证明:连接FO,

∵AN=AC,
∴∠CAN=∠CNA
∵AC∥ME,
∴∠CAN=∠MFN
∵∠CNA=∠FNM
∴∠MFN=∠FNM=∠CAN
又∵CD⊥AB,
∴∠HAN+∠HNA=90°,
∵AO=FO,
∴∠OAF=∠OFA
∴∠OFA+∠MFN=90°,即∠MFO=90°,
∴直线ME与圆O相切
(2)解:连接OC,
∵AC:CD=5:8,设AC=5 a,则CD=8 a,
∵CD⊥AB,
∴CH=DH=4 a,AH=3 a,
∵CA=CN,
∴NH= a,
∴AN= ![]() ,
,
∴ a=3,AH=3, a=9,CH=4 ,a=12.
设圆的半径为r,则OH=r﹣9,
在Rt△OCH中,OC=r,CH=12,OH=r﹣9,
由OC2=CH2+OH2得 ![]() ,
,
解得:r= ![]() ,
,
∴圆O的直径的长度为2r=25
(3)连接BF,根据(2)
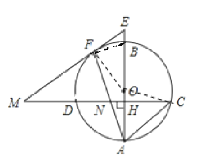
可得△ANH∽△ABF
∴![]() 可得
可得![]()
解得AF=![]()
∵FN=AF-AN=![]() -3
-3![]() =
=![]()
∴FN= ![]()


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解七年级学生体育测试情况,以七年级(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下的统计图,请你结合图中所给的信息解答下列问题:

(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所在的扇形的圆心角度数是 ;
(3)若该校七年级有600名学生,请用样本估计体育测试中A级学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
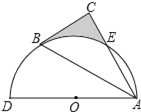
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,弧BE的长为![]() π,则图中阴影部分的面积为( )
π,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
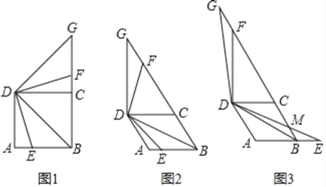
【题目】(1)如图1,E是正方形ABCD边AB上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转90°,旋转后角的两边分别与射线BC交于点F和点G.
①线段DB和DG的数量关系是 ;
②写出线段BE,BF和DB之间的数量关系.
(2)当四边形ABCD为菱形,∠ADC=60°,点E是菱形ABCD边AB所在直线上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转120°,旋转后角的两边分别与射线BC交于点F和点G.
①如图2,点E在线段AB上时,请探究线段BE、BF和BD之间的数量关系,写出结论并给出证明;
②如图3,点E在线段AB的延长线上时,DE交射线BC于点M,若BE=1,AB=2,直接写出线段GM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
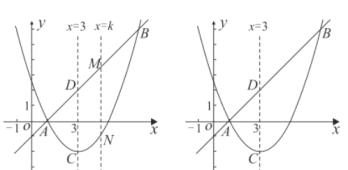
【题目】已知抛物线![]() 的顶点为点
的顶点为点![]() .
.
(1)求证:不论![]() 为何实数,该抛物线与
为何实数,该抛物线与![]() 轴总有两个不同的交点;
轴总有两个不同的交点;
(2)若抛物线的对称轴为直线![]() ,求
,求![]() 的值和
的值和![]() 点坐标;
点坐标;
(3)如图,直线![]() 与(2)中的抛物线并于
与(2)中的抛物线并于![]() 两点,并与它的对称轴交于点
两点,并与它的对称轴交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .求当
.求当![]() 为何值时,以
为何值时,以![]() 为顶点的四边形为平行四边形.
为顶点的四边形为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,5辆大货车与3辆小货车一次可以运货21吨,3辆大货车与2辆小货车一次可以运货13吨.
(1)每辆大货车和每辆小货车一次各可以运货多少吨?
(2)现有这两种货车共10辆,要求一次运货不低于23吨,则其中大货车至少多少辆?
(3)日前有20吨货物需要运输,欲租用这两种货车运送,要求全部货物一次运完且每辆车必须装满.已知每辆大货车一次运货租金为400元,每辆小货车一次运货租金为200元,请列出所有的运输方案井求出最少租金
查看答案和解析>>
科目:初中数学 来源: 题型:
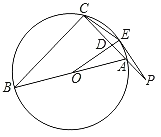
【题目】如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PAPC,连接CE,AE,OE,OE交CA于点D.
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°,![]() ,求证:DO=DP.
,求证:DO=DP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角度数为α,看这栋楼底部C处的俯角度数为β,热气球A处与楼的水平距离为100m,则这栋楼的高度表示为( )
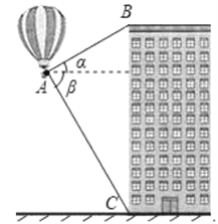
A.100(tanα+tanβ)mB.100(sinα+sinβ)mC.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com