
【题目】有大小两种货车,5辆大货车与3辆小货车一次可以运货21吨,3辆大货车与2辆小货车一次可以运货13吨.
(1)每辆大货车和每辆小货车一次各可以运货多少吨?
(2)现有这两种货车共10辆,要求一次运货不低于23吨,则其中大货车至少多少辆?
(3)日前有20吨货物需要运输,欲租用这两种货车运送,要求全部货物一次运完且每辆车必须装满.已知每辆大货车一次运货租金为400元,每辆小货车一次运货租金为200元,请列出所有的运输方案井求出最少租金
【答案】(1)1辆大货车和1辆小货车一次可以分别运货3吨、2吨;(2)至少需要安排3辆大货车;(3)共有3中运输方案,方案1:租用2辆大货车,7辆小货车;方案2:租用4辆大货车,4辆小货车;方案3:租用6辆大货车,1辆小货车;最少租金为2200元,应选择方案1,即租用2辆大货车,7辆小货车
【解析】
(1)设每辆大货车一次可以运货x吨,每辆小货车一次可以运货y吨,根据“5辆大货车与3辆小货车一次可以运货21吨,3辆大货车与2辆小货车一次可以运货13吨”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设大货车有m辆,则小货车有(10-m)辆,根据运货总量=3×大货车的辆数+2×小货车的辆数结合货物总量不低于23吨,即可得出关于m的一元一次不等式,解之取其中的最小整数值即可得出结论;
(3)设租用a辆大货车,租用b辆小货车,根据运货总量=3×大货车的辆数+2×小货车的辆数,即可得出关于a,b的二元一次方程,结合a,b均为非负整数即可求出a,b的值,进而可得出各运输方案,再求出各方案所需租金,比较后即可得出结论.
解:(1)设1辆大货车和1辆小货车一次可以分别运货x吨、y吨,
根据题意,得:![]() ,
,
解得:![]() ,
,
答:1辆大货车和1辆小货车一次可以分别运货3吨、2吨;
(2)解:设安排m辆大货车,则小货车需要(10-m)辆,
根据题意,得:3m+2(10-m)≥23,
解得:m≥3,
所以至少需要安排3辆大货车;
(3)解:设租大货车a辆,小货车b辆,由题意得3a+2b=20,
∵a,b为非负整数,
∴![]() ,
,![]() ,
,![]() ,
,
∴共有3中运输方案,方案1:租用2辆大货车,7辆小货车;方案2:租用4辆大货车,4辆小货车;方案3:租用6辆大货车,1辆小货车,
方案1的租金:400×2+200×7=2200元,
方案2的租金:400×4+200×4=2400元,
方案3的租金:400×6+200×1=2600元
∵2200<2400<2600,
∴最少租金为2200元,应选择方案1,即租用2辆大货车,7辆小货车.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
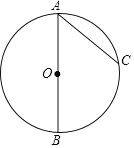
【题目】如图,AB是⊙O的直径,C是⊙O上一点,连接AC.过点B作⊙O的切线,交AC的延长线于点D,在AD上取一点E,使AE=AB,连接BE,交⊙O于点F.
请补全图形并解决下面的问题:
(1)求证:∠BAE=2∠EBD;
(2)如果AB=5,sin∠EBD=![]() .求BD的长.
.求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
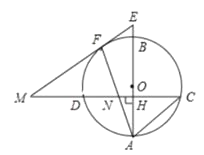
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,在CD上有点N满足CN=CA,AN交圆O于点F,过点F的AC的平行线交CD的延长线于点M,交AB的延长线于点E.
(1)求证:EM是圆O的切线;
(2)若AC:CD=5:8,AN=3![]() ,求圆O的直径长度.
,求圆O的直径长度.
(3)在(2)的条件下,直接写出FN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=16.点D在边BC上,且点D到边AB和边AC的距离相等.
(1)用直尺和圆规作出点D(不写作法,保留作图痕迹,在图上标注出点D);
(2)求点D到边AB的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.
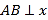
查看答案和解析>>
科目:初中数学 来源: 题型:
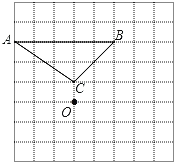
【题目】如图,已知△ABC和点O.
(1)把△ABC绕点O顺时针旋转90°得到△A1B1C1,在网格中画出△A1B1C1;
(2)用直尺和圆规作△ABC的边AB,AC的垂直平分线,并标出两条垂直平分线的交点P(要求保留作图痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过A(-1,0)、B(4,5)三点.
的图象经过A(-1,0)、B(4,5)三点.
(1)求此二次函数的解析式;
(2)当x为何值时,y随x的增大而减小?
(3)当x为何值时,y>0?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com