
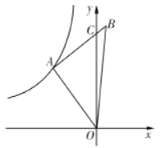
【题目】如图,点![]() 在反比例函数
在反比例函数![]()
![]() 的图象上,连接
的图象上,连接![]() ,作
,作![]() ,且
,且![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
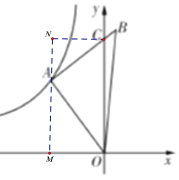
过A作AM⊥x轴于M,作CN⊥AM,交MA延长线于N,根据![]() ,△COB的面积
,△COB的面积![]() ,易求得△AOC的面积为
,易求得△AOC的面积为![]() ,进而求得S△AOM+S△ANC=S△AOC=
,进而求得S△AOM+S△ANC=S△AOC=![]() ,通过证得△OAM∽△ACN,得出
,通过证得△OAM∽△ACN,得出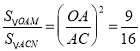 ,即可求得S△OBM=
,即可求得S△OBM=![]() =6,根据反比例函数系数k的几何意义,即可确定k的值.
=6,根据反比例函数系数k的几何意义,即可确定k的值.
解:过A作AM⊥x轴于M,作CN⊥AM,交MA延长线于N,
∵![]() ,△COB的面积
,△COB的面积![]()
∴S△AOC=3S△COB=![]()
∵四边形OMNC是矩形
∴S△AOM+S△ANC=S△AOC=![]()
∵![]() ,且AO=AB,
,且AO=AB,
∴∠CAN+∠OAM=90°,∠AOM+∠OAM=90°,
∴∠AOM=∠CAN,
又∵∠AMO=∠CNA=90°,
∴△OAM∽△ACN,
∴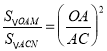
∵BC∶AC =1:3,
∴OA∶AC =4:3,
∴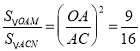
∴S△OAM=![]() =6
=6
∵点B在反比例函数![]()
![]() 的图象上,
的图象上,
∴S△OBM=![]() |k|,解得k=±12
|k|,解得k=±12
∵图象在第二象限,
.∴k=-12.
故答案为B.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若sin∠OAB=![]() ,求点M的坐标;
,求点M的坐标;
(3)在(2)的条件下,直接写出以点O、M、B为其中三个顶点的平行四边形的第四个顶点P的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:![]() ,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() 取1.73.
取1.73.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学实践活动中,观测小组对某品牌节能饮水机进行了观察和记录,当观察到第![]() 分钟时,水温为
分钟时,水温为![]() ,记录的相关数据如下表所示:
,记录的相关数据如下表所示:
第一次加热、降温过程 | … | |||||||||||
t(分钟) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | … |
y( | 20 | 40 | 60 | 80 | 100 | 80 | 66.7 | 57.1 | 50 | 44.4 | 40 | … |
(饮水机功能说明:水温加热到![]() 时饮水机停止加热,水温开始下降,当降到
时饮水机停止加热,水温开始下降,当降到![]() 时饮水机又自动开始加热)
时饮水机又自动开始加热)
请根据上述信息解决下列问题:
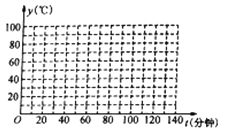
(1)根据表中数据在如给出的坐标系中,描出相应的点;
(2)选择适当的函数,分别求出第一次加热过程和第一次降温过程![]() 关于
关于![]() 的函数关系式,并写出相应自变量的取值范围;
的函数关系式,并写出相应自变量的取值范围;
(3)已知沏茶的最佳水温是![]() ,若18:00开启饮水机(初始水温
,若18:00开启饮水机(初始水温![]() )到当晚20:10,沏茶的最佳水温时间共有多少分钟?
)到当晚20:10,沏茶的最佳水温时间共有多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
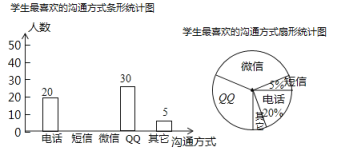
(1)这次统计共抽查了多少名学生?在扇形统计图中,表示" ![]() "的扇形圆心角的度数是多少;
"的扇形圆心角的度数是多少;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用 “微信”进行沟通的学生大约有多少名?
(4)某天甲、乙两名同学都想从“微信"、"![]() "、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
"、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解七年级学生体育测试情况,以七年级(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下的统计图,请你结合图中所给的信息解答下列问题:

(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所在的扇形的圆心角度数是 ;
(3)若该校七年级有600名学生,请用样本估计体育测试中A级学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,5辆大货车与3辆小货车一次可以运货21吨,3辆大货车与2辆小货车一次可以运货13吨.
(1)每辆大货车和每辆小货车一次各可以运货多少吨?
(2)现有这两种货车共10辆,要求一次运货不低于23吨,则其中大货车至少多少辆?
(3)日前有20吨货物需要运输,欲租用这两种货车运送,要求全部货物一次运完且每辆车必须装满.已知每辆大货车一次运货租金为400元,每辆小货车一次运货租金为200元,请列出所有的运输方案井求出最少租金
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com