
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
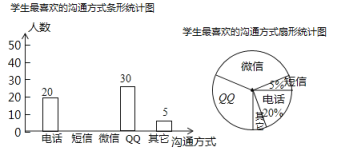
(1)这次统计共抽查了多少名学生?在扇形统计图中,表示" ![]() "的扇形圆心角的度数是多少;
"的扇形圆心角的度数是多少;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用 “微信”进行沟通的学生大约有多少名?
(4)某天甲、乙两名同学都想从“微信"、"![]() "、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
"、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
【答案】(1)100;108°;(2)详见解析;(3)600人;(4)![]()
【解析】
(1)利用喜欢“电话”沟通的人数除以其所占调查总人数的百分率即可求出调查总人数,然后求出喜欢“QQ” 沟通的人数占调查总人数的百分率,再乘360°即可求出结论;
(2)用调查总人数×喜欢“短信”沟通的人数所占百分率即可求出喜欢“短信”沟通的人数,然后用调查总人数减去其余“电话”、“短信”、“QQ”和“其它”沟通的人数即可求出喜欢用“微信”沟通的人数,最后补全条形统计图即可;
(3)先求出喜欢用“微信”沟通的人数占调查总人数的百分率,再乘1500即可;
(4)根据题意,画出树状图,然后根据概率公式计算即可.
解:(1)调查总人数为20÷20%=100人
表示" ![]() "的扇形圆心角的度数是30÷100×360°=108°
"的扇形圆心角的度数是30÷100×360°=108°
(2)喜欢用“短信”沟通的人数为:100×5%=5人,
喜欢用“微信”沟通的人数为:100-20-5-30-5=40人,
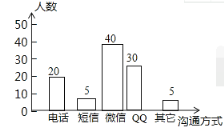
补充条形统计图,如图所示:
(3)喜欢用“微信”沟通所占百分比为:
![]()
∴该校共有1500名学生,估计该校最喜欢用“微信”进行沟通的学生有:
![]() 人.
人.
答:该校最喜欢用“微信”进行沟通的学生有600人.
(4)列出树状图,如图所示,

共有9种等可能的结果,其中两人恰好选中同一种沟通方式共有3种情况,
所以甲、乙两名同学恰好选中同一种沟通方式的概率为:![]()


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”“一般”“较强”“很强”四个层次,并绘制成如下两幅尚不完整的统计图
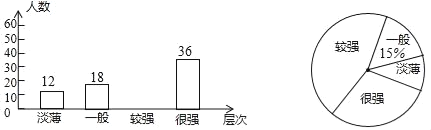
根据以上信息,解答下列问题:
(1)该校有1200名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有多少名?
(2)请直接将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
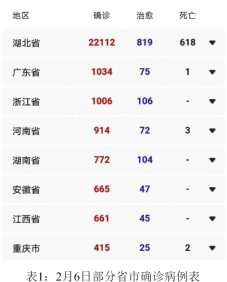
【题目】全国人民每天都很关心新型冠状病毒感染肺炎的全国疫情和湖北疫情,下面是2020年2月7日小明在网上看到的2020年2月6日有关全国和武汉的疫情统计图表:
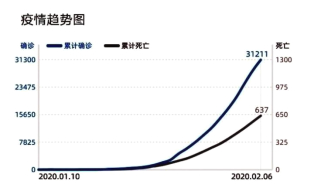
图1全国疫情趋势图
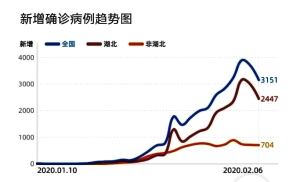
图2新增确诊病例趋势图
根据统计图表提供的信息,下列推断不合理的是( )
A.从图1可得出在2月6日的全国确诊病例达到3万多,是“非典”确诊病例(共5327例)的若干倍,说明新型冠状病毒比“非典”病毒传染性强.
B.从图2可得出在2月6日新增病例出现下降,说明此时全国的累计确诊病例开始下降,肺炎疫情得到控制,政府和人民的防疫工作有了显著成效
C.从图2在2月6日新增病例出现下降,可以估计2月6日后全国新型冠状病毒肺炎累计确诊病例的单日增长率会低于10%.
D.从表1可看出确诊病例较多的省市大部分都是在湖北周围,很大原因是由于携带病毒的流动人口造成的,所以控制疫情的有效手段是在家隔离,同时也可以推断在新疆和甘肃等西北地区疫情相对缓和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于A,B两点,其中点B的坐标为B(4,0),抛物线的对称轴交x轴于点D,CE∥AB,并与抛物线的对称轴交于点E.现有下列结论:①a>0;②b>0;③4a+2b+c<0;④AD+CE=4.其中所有正确结论的序号是( )
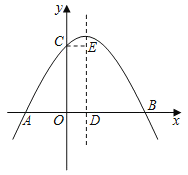
A.①②B.①③C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象经过点C(0,-2),顶点D的坐标为(1,
的图象经过点C(0,-2),顶点D的坐标为(1,![]() ),与
),与![]() 轴交于A、B两点.
轴交于A、B两点.
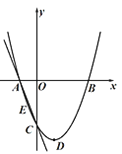
(1)求抛物线的解析式.
(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和![]() 的值.
的值.
(3)点F(0,![]() )是
)是![]() 轴上一动点,当
轴上一动点,当![]() 为何值时,
为何值时,![]() 的值最小.并求出这个最小值.
的值最小.并求出这个最小值.
(4)点C关于![]() 轴的对称点为H,当
轴的对称点为H,当![]() 取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
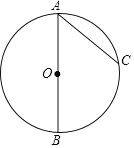
【题目】如图,AB是⊙O的直径,C是⊙O上一点,连接AC.过点B作⊙O的切线,交AC的延长线于点D,在AD上取一点E,使AE=AB,连接BE,交⊙O于点F.
请补全图形并解决下面的问题:
(1)求证:∠BAE=2∠EBD;
(2)如果AB=5,sin∠EBD=![]() .求BD的长.
.求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
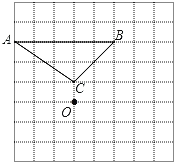
【题目】如图,已知△ABC和点O.
(1)把△ABC绕点O顺时针旋转90°得到△A1B1C1,在网格中画出△A1B1C1;
(2)用直尺和圆规作△ABC的边AB,AC的垂直平分线,并标出两条垂直平分线的交点P(要求保留作图痕迹,不写作法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com