
【题目】如图,抛物线![]() 的图象经过点C(0,-2),顶点D的坐标为(1,
的图象经过点C(0,-2),顶点D的坐标为(1,![]() ),与
),与![]() 轴交于A、B两点.
轴交于A、B两点.
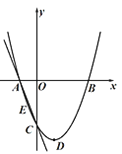
(1)求抛物线的解析式.
(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和![]() 的值.
的值.
(3)点F(0,![]() )是
)是![]() 轴上一动点,当
轴上一动点,当![]() 为何值时,
为何值时,![]() 的值最小.并求出这个最小值.
的值最小.并求出这个最小值.
(4)点C关于![]() 轴的对称点为H,当
轴的对称点为H,当![]() 取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)E
;(2)E![]() ,
,![]() ;(3)当
;(3)当![]() 时,
时,![]() 有最小值为
有最小值为![]() ;(4)存在,点Q的坐标为
;(4)存在,点Q的坐标为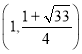 或
或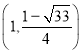 或
或![]() 或
或![]() .
.
【解析】
(1)把C、D坐标代入二次函数解析式,列方程组求出a、c的值即可;(2)根据抛物线解析式可求出A、B两点坐标,即可求出AC、AB的长,设直线AC的解析式为:![]() ,把A、C坐标代入可求出k、b的值,可得直线AC的解析式,根据△AOC∽△AEB可得
,把A、C坐标代入可求出k、b的值,可得直线AC的解析式,根据△AOC∽△AEB可得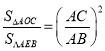 ,可求出△AEB的面积,进而可求出
,可求出△AEB的面积,进而可求出![]() ,代入直线AC解析式可求出E点坐标,根据相似三角形的性质即可求出
,代入直线AC解析式可求出E点坐标,根据相似三角形的性质即可求出![]() 的值;(3)连接BF,过点F作FG⊥AC于G,可得FG=
的值;(3)连接BF,过点F作FG⊥AC于G,可得FG=![]() ,可得当折线段BFG与BE重合时,取得最小值,由(2)可知∠ABE=∠ACO,利用∠ABE的余弦和正切求出BE的长和
,可得当折线段BFG与BE重合时,取得最小值,由(2)可知∠ABE=∠ACO,利用∠ABE的余弦和正切求出BE的长和 ![]() 的值即可;(4)可分如下三种情况:当点Q为直角顶点时(如图):由(3)可知F点的坐标,根据点C与点H关于
的值即可;(4)可分如下三种情况:当点Q为直角顶点时(如图):由(3)可知F点的坐标,根据点C与点H关于![]() 轴对称可求出点H坐标,设Q(1,
轴对称可求出点H坐标,设Q(1,![]() ),过点Q作QM
),过点Q作QM![]()
![]() 轴于点M,可得Rt△QHM∽Rt△FQM,即可证明
轴于点M,可得Rt△QHM∽Rt△FQM,即可证明![]() ,即可求出m的值;当点H为直角顶点时,可得HQ//x轴,即可得出Q点坐标,当点F为直角顶点时,可得FQ//x轴,即可求出Q点坐标.
,即可求出m的值;当点H为直角顶点时,可得HQ//x轴,即可得出Q点坐标,当点F为直角顶点时,可得FQ//x轴,即可求出Q点坐标.
(1)∵![]() 的图象经过点C(0,-2),顶点D的坐标为(1,
的图象经过点C(0,-2),顶点D的坐标为(1,![]() ),
),
∴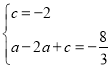 ,
,
解得: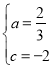 ,
,
∴抛物线解析式为:![]() .
.
(2)∵抛物线解析式为:![]() .
.
∴当y=0时,![]() =0,
=0,
解得:x1=-1,x2=3,
∴OA=1,OB=3,AB=4,
∵C(0,-2),
∴OC=2,
∴AC=![]() ,
,
设直线AC的解析式为:![]() ,则
,则![]()
解得:![]()
∴直线AC的解析式为:![]()
当△AOC∽△AEB时(如图)
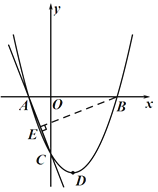
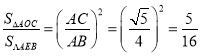
∵![]()
∴![]()
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴E![]() ,
,
∵△AOC∽△AEB,
∴![]() ,
,
∴![]() ,
,
(3)如图,连接BF,过点F作FG⊥AC于G
则FG=![]() ,
,
∴![]() ,
,
当折线段BFG与BE重合时,取得最小值,
由(2)可知∠ABE=∠ACO,
∴![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() 有最小值为
有最小值为![]() .
.

(4)可分如下三种情况:
①当点Q为直角顶点时(如图):
由(3)得F![]() ,
,
∵C(0,-2),
∴H(0,2),
∵点Q在抛物线的对称轴上,
∴设Q(1,![]() ),
),
过点Q作QM![]()
![]() 轴于点M,
轴于点M,
则Rt△QHM∽Rt△FQM,
∴![]() ,
,
∴![]() ,
,
即![]()
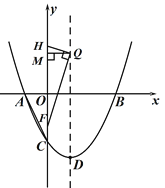
∴Q(1,![]() )或Q(1,
)或Q(1,![]() ),
),
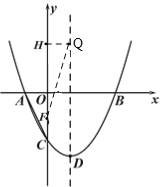
②如图,当点H为直角顶点时:
∵∠FHQ=90°,
∴HQ//x轴,
∵H(0,2),Q点在抛物线对称轴上,
∴Q(1,2),
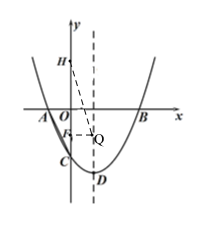
③如图,当点F为直角顶点时,
∵∠HFQ=90°,
∴FQ//x轴,
∵F(0,![]() ),Q点在抛物线对称轴上,
),Q点在抛物线对称轴上,
∴Q(1,![]() ).
).
综上所述,点Q的坐标为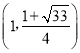 或
或 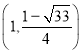 或
或 ![]() 或
或![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
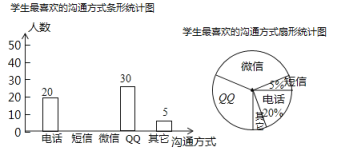
(1)这次统计共抽查了多少名学生?在扇形统计图中,表示" ![]() "的扇形圆心角的度数是多少;
"的扇形圆心角的度数是多少;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用 “微信”进行沟通的学生大约有多少名?
(4)某天甲、乙两名同学都想从“微信"、"![]() "、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
"、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
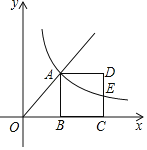
【题目】如图,点A是射线y═![]() (x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=
(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=![]() 交CD边于点E,则
交CD边于点E,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解七年级学生体育测试情况,以七年级(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下的统计图,请你结合图中所给的信息解答下列问题:

(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所在的扇形的圆心角度数是 ;
(3)若该校七年级有600名学生,请用样本估计体育测试中A级学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
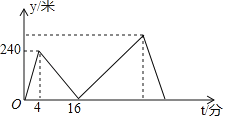
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
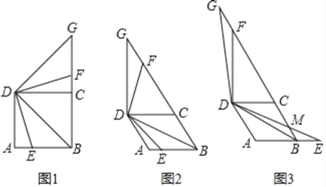
【题目】(1)如图1,E是正方形ABCD边AB上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转90°,旋转后角的两边分别与射线BC交于点F和点G.
①线段DB和DG的数量关系是 ;
②写出线段BE,BF和DB之间的数量关系.
(2)当四边形ABCD为菱形,∠ADC=60°,点E是菱形ABCD边AB所在直线上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转120°,旋转后角的两边分别与射线BC交于点F和点G.
①如图2,点E在线段AB上时,请探究线段BE、BF和BD之间的数量关系,写出结论并给出证明;
②如图3,点E在线段AB的延长线上时,DE交射线BC于点M,若BE=1,AB=2,直接写出线段GM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】象棋是棋类益智游戏,中国象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.李凯和张萌利用象棋棋盘和棋子做游戏.李凯将四枚棋子反面朝上放在棋盘上,其中有两个“兵”、一个“马”、一个“士”,张萌随机从这四枚棋子中摸一枚棋子,记下正汉字,然后再从剩下的三枚棋子中随机摸一枚.
(1)求张萌第一次摸到的棋子正面上的汉字是“兵”的概率;
(2)游戏规定:若张萌两次摸到的棋子中有“士”,则张萌胜;否则,李凯胜.请你用树状图或列表法求李凯胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com