
【题目】如图,三角形 ABC 是由三角形 ABC 经过某种平移得到的,点 A 与点 A ,点 B与点B ,点C与点C分别对应,且这六个点都在格点上,观察各点以及各点坐标之间的关系,解答下列问题:
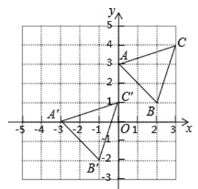
①分别写出点 B 和点B 的坐标,并说明三角形ABC 是由三角形 ABC 经过怎样的平移得到的;
②连接 BC ,直接写出 ∠ CBC 与∠ BCO 之间的数量关系 ;
③若点 M(a-1,2b﹣5)是三角形 ABC 内一点,它随三角形 ABC 按(1)中方式平移后得到的对应点为点 N(2a﹣7,4-b),求 a 和 b 的值.
【答案】①B(2,1),![]() (-1,-2)
(-1,-2)
三角形ABC 是由三角形 ABC先向左平移3个单位长度,再向下平移3个单位长度得到的(或先向下平移3个单位长度,再向左平移3个单位长度得到的);
②∠ CBC∠ BCO+![]()
③a=3,b=4
【解析】
①根据坐标与图形的性质确定对应点的坐标,找出对应点的横纵坐标之间的关系.
②根据平移的性质即可求解.
③根据对应点的横纵坐标之间的关系列出方程组,解方程组即可.
解:①B(2,1),![]() (-1,-2)
(-1,-2)
三角形ABC 是由三角形 ABC先向左平移3个单位长度,再向下平移3个单位长度得到的(或先向下平移3个单位长度,再向左平移3个单位长度得到的).
②∵三角形 ABC 是由三角形 ABC 经过某种平移得到的
∴∠ CBC∠ BCO+![]()
③由①中的平移变换得,
a-1-3=2a﹣7
a=3
2b﹣5-3=4-b
b=4


科目:初中数学 来源: 题型:
【题目】已知方程组![]() 的解x为非正数,y为负数.
的解x为非正数,y为负数.
(1)求a的取值范围;
(2)化简∣a-3∣+∣a+2∣;
(3)在a的取值范围内,m是最大的整数,n是最小的整数,求(m+n)m-n的值;
(4)在a的取值范围内,当a取何整数时,不等式2ax+x>2a+1的解为x<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、DEFG都是正方形,连接AE,CG.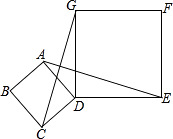
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,将矩形ABCD绕B逆时针旋转30°后得到矩形GBEF,延长DA交FG于点H,则GH的长为( )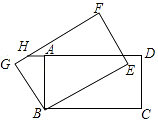
A.8﹣4 ![]()
B.![]() ﹣4
﹣4
C.3 ![]() ﹣4
﹣4
D.6﹣3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知线段 AB 的两个端点坐标分别为A(a,5),B(8,b),且![]() .
.

(1)求 a,b 的值;
(2)①连OA,OB,则SAOB = 平方单位;(说明:SAOB 表示三角形 AOB 的面积,下同.)
②点P从O点出发沿 y 轴负方向运动,速度为每秒1个单位,连PA交OB于C,则运动多少秒时,SABC=SPOC ;
(3)在(2)的条件下,过P作直线m∥AB,过B作直线 l∥x轴,直线m和直线l相交于点Q,请直接写出点Q的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”小长假期间,某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性购物满500元以上均可获得两次摸球的机会(摸出小球后放回).超市根据两小球所标金额的和返还相应的代金券.
(1)顾客甲购物1000元,则他最少可获元代金券,最多可获元代金券.
(2)请用树形图或列表方法,求出顾客甲获得不低于30元(含30元)代金券的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.
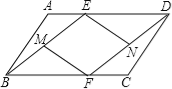
(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明今年五一节去三峡广场逛水果超市,他分两次购进了![]() 、
、![]() 两种不同单价的水果.第一次购买
两种不同单价的水果.第一次购买![]() 种水果的数量比
种水果的数量比![]() 种水果的数量多50%,第二次购买
种水果的数量多50%,第二次购买![]() 种水果的数量比第一次购买
种水果的数量比第一次购买![]() 种水果的数量少60%,结果第二次购买水果的总数量比第一次购买水果的总数量多20%,且第二次购买
种水果的数量少60%,结果第二次购买水果的总数量比第一次购买水果的总数量多20%,且第二次购买![]() 、
、![]() 水果的总费用比第一次购买
水果的总费用比第一次购买![]() 、
、![]() 水果的总费用少10%(两次购买中
水果的总费用少10%(两次购买中![]() 、
、![]() 两种水果的单价不变),则
两种水果的单价不变),则![]() 种水果的单价与
种水果的单价与![]() 种水果的单价的比值是______.
种水果的单价的比值是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com