
【题目】如图,四边形ABCD、DEFG都是正方形,连接AE,CG.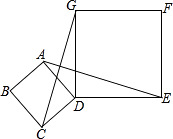
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
【答案】
(1)证明:如图, 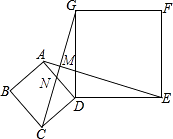
∵AD=CD,DE=DG,∠ADC=∠GDE=90°,
又∵∠CDG=90°+∠ADG=∠ADE,
∴△ADE≌△CDG(SAS).
∴AE=CG.
(2)猜想:AE⊥CG.
证明:如图,设AE与CG交点为M,AD与CG交点为N.
∵△ADE≌△CDG,
∴∠DAE=∠DCG.
又∵∠ANM=∠CND,
∴△AMN∽△CDN.
∴∠AMN=∠ADC=90°.
∴AE⊥CG
【解析】(1)首先依据正方形的性质得到AD=CD,DE=DG,∠ADC=∠GDE=90°,然后再依据等式的性质证明∠CDG=∠ADE,接下来,依据SAS可证明△ADE≌△CDG,从而可得到AE=CG;
(2)由全等三角形的性质可得到∠DAE=∠DCG,然后可证明△AMN∽△CDN,最后,依据相似三角形对应角相等可得到∠AMN=∠ADC=90°.
【考点精析】根据题目的已知条件,利用正方形的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10, ![]() =
= ![]() =
= ![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )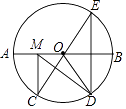
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
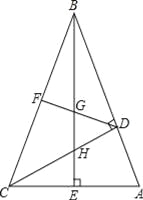
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2﹣GE2=EA2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
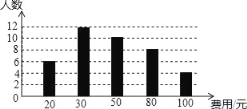
【题目】在全民读书月活动中,某校随机调查了40名同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题,直接写出结果.
(1)这次调查获取的样本数据的众数是 .
(2)这次调查获取的样本数据的中位数是 .
(3)若该校共有1200名学生,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形 ABC 是由三角形 ABC 经过某种平移得到的,点 A 与点 A ,点 B与点B ,点C与点C分别对应,且这六个点都在格点上,观察各点以及各点坐标之间的关系,解答下列问题:
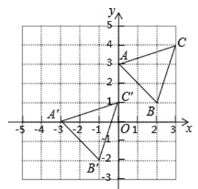
①分别写出点 B 和点B 的坐标,并说明三角形ABC 是由三角形 ABC 经过怎样的平移得到的;
②连接 BC ,直接写出 ∠ CBC 与∠ BCO 之间的数量关系 ;
③若点 M(a-1,2b﹣5)是三角形 ABC 内一点,它随三角形 ABC 按(1)中方式平移后得到的对应点为点 N(2a﹣7,4-b),求 a 和 b 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,点O也是正方形A′B′C′O的一个顶点,如果两个正方形的边长都等于1,那么正方形A′B′C′O绕顶点O转动,两个正方形重叠部分的面积大小有什么规律?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com