
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10, ![]() =
= ![]() =
= ![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )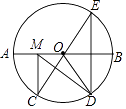
A.1
B.2
C.3
D.4
【答案】C
【解析】∵ ![]() =
= ![]() =
= ![]() ,点E是点D关于AB的对称点,
,点E是点D关于AB的对称点,
∴ ![]() =
= ![]() ,
,
∴∠DOB=∠BOE=∠COD= ![]() =60°,∴①正确;
=60°,∴①正确;
∠CED= ![]() ∠COD=
∠COD= ![]() =30°=
=30°= ![]() ,∴②正确;
,∴②正确;
∵ ![]() 的度数是60°,
的度数是60°,
∴ ![]() 的度数是120°,
的度数是120°,
∴只有当M和A重合时,∠MDE=60°,
∵∠CED=30°,
∴只有M和A重合时,DM⊥CE,∴③错误;
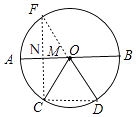
做C关于AB的对称点F,连接CF,交AB于N,连接DF交AB于M,此时CM+DM的值最短,等于DF长,
连接CD,
∵ ![]() =
= ![]() =
= ![]() =
= ![]() ,并且弧的度数都是60°,
,并且弧的度数都是60°,
∴∠D= ![]() =60°,∠CFD=
=60°,∠CFD= ![]() =30°,
=30°,
∴∠FCD=180°﹣60°﹣30°=90°,
∴DF是⊙O的直径,
即DF=AB=10,
∴CM+DM的最小值是10,∴④正确;
故答案为:C.
由已知条件求出,求出∠DOB=∠COD=∠BOE=60°,求出∠CED,即可判断①②;根据圆周角定理求出当M和A重合时∠MDE=60°即可判断③;求出M点的位置,根据圆周角定理得出此时DF是直径,即可求出DF长,即可判断④,最后得到所求的结论..


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE =12,CE =5,则平行四边形ABCD的周长是______.
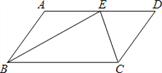
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把三角形ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
(1)画出△A′B′C′;并直接写出点A′、B′、C′的坐标;
(2)若点P(m,n)是△ABC某边上的点,经上述平移后,点P的对应点为P′,写出点P′的坐标(用含m,n的式子表示).
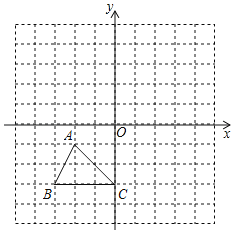
查看答案和解析>>
科目:初中数学 来源: 题型:
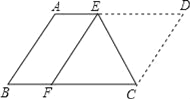
【题目】如图,将ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
(1)求证:四边形ABFE为平行四边形;
(2)若AB=4,BC=6,求四边形ABFE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.
例如:分解因式![]() ;求代数式
;求代数式![]() 的最小值,
的最小值,![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _______.
_______.
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最大值?并求出这个最大值.
有最大值?并求出这个最大值.
(3)利用配方法,尝试解方程![]() ,并求出
,并求出![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
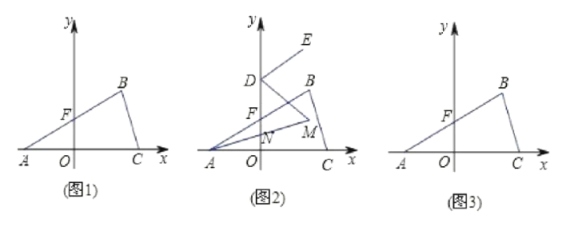
【题目】如(图1),在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,且满足
,且满足![]() ,线段
,线段![]() 交
交![]() 轴于
轴于![]() 点.
点.
(1)填空:![]() ,
,![]() ;
;
(2)点![]() 为
为![]() 轴正半轴上一点,若
轴正半轴上一点,若![]() ,
,![]() ,且
,且![]() 分别平分
分别平分![]() ,如(图2),求
,如(图2),求![]() 的度数;
的度数;
(3)求点![]() 的坐标;
的坐标;
(4)如(图3),在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使三角形
,使三角形![]() 的面积和三角形
的面积和三角形![]() 的面积相等?若存在,求出
的面积相等?若存在,求出![]() 点坐标,若不存在,说明理由.
点坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程组![]() 的解x为非正数,y为负数.
的解x为非正数,y为负数.
(1)求a的取值范围;
(2)化简∣a-3∣+∣a+2∣;
(3)在a的取值范围内,m是最大的整数,n是最小的整数,求(m+n)m-n的值;
(4)在a的取值范围内,当a取何整数时,不等式2ax+x>2a+1的解为x<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、DEFG都是正方形,连接AE,CG.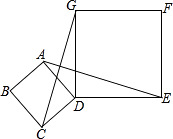
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com