
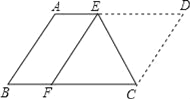
【题目】如图,将ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
(1)求证:四边形ABFE为平行四边形;
(2)若AB=4,BC=6,求四边形ABFE的周长.
【答案】(1)证明见解析;(2)12.
【解析】
(1)根据折叠的性质得到EF=ED,∠CFE=∠CDE,根据平行四边形的性质得到AD∥BC,∠B=∠D,由平行线的判定得到AE∥BF,即可得到结论;
(2)根据平行四边形的性质得到EF=AB=4.求得ED=4,得到AE=BF=6-4=2,于是得到结论.
(1)证明:∵将ABCD沿CE折叠,使点D落在BC边上的F处,∴EF=ED,∠CFE=∠CDE,
∵四边形ABCD是平行四边形,∴AD∥BC,∠B=∠D,∴AE∥BF,∠B=∠CFE,
∴AB∥EF,∴四边形ABFE为平行四边形;
(2)解:∵四边形ABFE为平行四边形,∴EF=AB=4,
∵EF=ED,∴ED=4,∴AE=BF=6﹣4=2,∴四边形ABFE的周长=AB+BF+EF+EA=12.


科目:初中数学 来源: 题型:
【题目】已知抛物线:y=ax2+bx+c(a>0)经过A(﹣1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论: ①b<1;②c<2;③0<m< ![]() ;④n≤1.
;④n≤1.
则所有正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).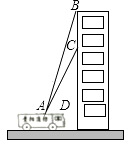
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年6月2日,贵阳市生态委发布了《2016年贵阳市环境状况公报》,公报显示,2016年贵阳市生态环境质量进一步提升,小颖根据公报中的部分数据,制成了下面两幅统计图,请根据图中提供的信息,回答下列问题: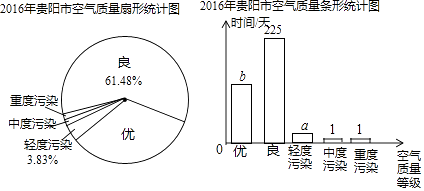
(1)a= , b=;(结果保留整数)
(2)求空气质量等级为“优”在扇形统计图中所占的圆心角的度数;(结果精确到1°)
(3)根据了解,今年1~5月贵阳市空气质量优良天数为142天,优良率为94%,与2016年全年的优良率相比,今年前五个月贵阳市空气质量的优良率是提高还是降低了?请对改善贵阳市空气质量提一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10, ![]() =
= ![]() =
= ![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )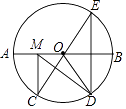
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“![]() ”方向排列,如
”方向排列,如![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .根据这个规律探索可得,第110个点的坐标为__________.
.根据这个规律探索可得,第110个点的坐标为__________.
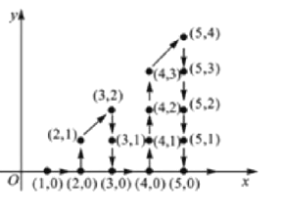
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.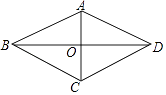
(1)求证:四边形ABCD是菱形;
(2)若CD=3,BD=2 ![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com