
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).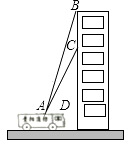
科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划新购进A,B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种树苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.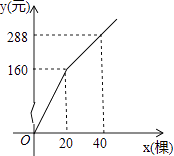
(1)求y与x的函数关系式;
(2)若在购买计划中,B种树苗的数量不超过35棵,但不少于A种树苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
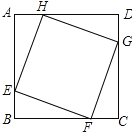
A. 30 B. 34 C. 36 D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
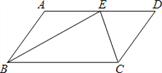
【题目】如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE =12,CE =5,则平行四边形ABCD的周长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
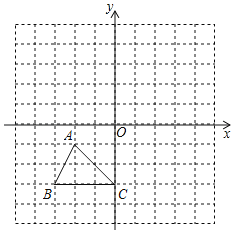
【题目】如图,把三角形ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
(1)画出△A′B′C′;并直接写出点A′、B′、C′的坐标;
(2)若点P(m,n)是△ABC某边上的点,经上述平移后,点P的对应点为P′,写出点P′的坐标(用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
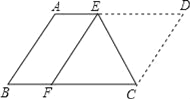
【题目】如图,将ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
(1)求证:四边形ABFE为平行四边形;
(2)若AB=4,BC=6,求四边形ABFE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
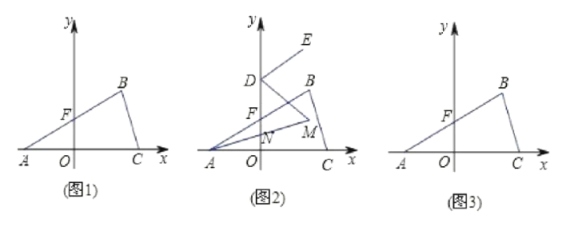
【题目】如(图1),在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,且满足
,且满足![]() ,线段
,线段![]() 交
交![]() 轴于
轴于![]() 点.
点.
(1)填空:![]() ,
,![]() ;
;
(2)点![]() 为
为![]() 轴正半轴上一点,若
轴正半轴上一点,若![]() ,
,![]() ,且
,且![]() 分别平分
分别平分![]() ,如(图2),求
,如(图2),求![]() 的度数;
的度数;
(3)求点![]() 的坐标;
的坐标;
(4)如(图3),在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使三角形
,使三角形![]() 的面积和三角形
的面积和三角形![]() 的面积相等?若存在,求出
的面积相等?若存在,求出![]() 点坐标,若不存在,说明理由.
点坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com