
分析 (1)观察已知等式,将原式进行适当变形得到结果,验证即可;
(2)归纳总结得到一般性规律,写出结果,验证即可.
解答 解:(1)根据题意得:$\sqrt{\frac{1}{4}(\frac{1}{5}-\frac{1}{6})}$=$\frac{1}{5}$$\sqrt{\frac{5}{24}}$,
等式左边=$\sqrt{\frac{1}{4}×\frac{1}{30}}$=$\sqrt{\frac{1}{120}}$,右边=$\frac{1}{5}$$\sqrt{\frac{25}{120}}$=$\sqrt{\frac{1}{120}}$,
左边=右边,成立;
(2)归纳总结得:$\sqrt{\frac{1}{n+1}(\frac{1}{n+2}-\frac{1}{n+3})}$=$\frac{1}{n+2}$$\sqrt{\frac{n+2}{(n+1)(n+3)}}$(n为正整数),
证明:等式左边=$\sqrt{\frac{1}{(n+1)(n+2)(n+3)}}$,右边=$\frac{1}{n+2}$$\sqrt{\frac{(n+2)^{2}}{(n+1)(n+2)(n+3)}}$=$\sqrt{\frac{1}{(n+1)(n+2)(n+3)}}$,
左边=右边,成立.
点评 此题考查了实数的运算,弄清题中的规律是解本题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
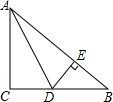 已知:如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△DEB的周长为10cm,求斜边AB的长.
已知:如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△DEB的周长为10cm,求斜边AB的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com