
【题目】如图,四边形OBCD中的三个顶点在⊙O上,点A是优弧BD上的一个动点(不与点B、D重合).
(1)当圆心O在∠BAD内部,∠ABO+∠ADO=50°时,∠A = °;
(2)当圆心O在∠BAD内部,四边形OBCD为平行四边形时,求∠C的度数;
(3)当圆心O在∠BAD外部,四边形OBCD为平行四边形时,请直接写出∠ABO与∠ADO的数量关系.

【答案】⑴500;(2)1200;(3)|∠ABO﹣∠ADO|=60°
【解析】
(1)连接OA,如图1,根据等腰三角形的性质得∠OAB=∠ABO,∠OAD=∠ADO,则∠BAD=∠OAB+∠OAD=∠ABO+∠ADO=50°;
(2)根据平行四边形的性质得∠BOD=∠BCD,再根据圆周角定理得∠BOD=2∠BAD,则∠BCD=2∠BAD,然后根据圆内接四边形的性质由∠BCD+∠BAD =180°,易计算出∠BAD的度数,从而得出结论;
(3)讨论:当∠OAB比∠ODA小时,如图2,与(1)一样∠OAB=∠ABO,∠OAD=∠ADO,则∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,由(2)得∠BAD=60°,所以∠ADO﹣∠ABO=60°;当∠OAB比∠ODA大时,用样方法得到∠ABO﹣∠ADO=60°.
(1)连接OA,如图1.
∵OA=OB,OA=OD.
∵∠OAB=∠ABO,∠OAD=∠ADO,∴∠BAD=∠OAB+∠OAD=∠ABO+∠ADO=50°;
(2)∵四边形OBCD为平行四边形,∴∠BOD=∠BCD.
∵∠BOD=2∠BAD,∴∠BCD=2∠BAD.
∵∠BCD+∠BAD =180°,即3∠BAD =180°,∴∠BAD =60°,∴∠C=180°-60°=120°;
(3)当∠OAB比∠ODA小时,如图2.
∵OA=OB,OA=OD.
∵∠OAB=∠ABO,∠OAD=∠ADO,∴∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,由(2)得∠BAD=60°,∴∠ADO﹣∠ABO=60°;
当∠OAB比∠ODA大时,同理可得∠ABO﹣∠ADO=60°.
综上所述:|∠ABO﹣∠ADO|=60°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
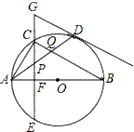
【题目】如图,在⊙O中,AB是⊙O的直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:①GP=GD;②∠BAD=∠ABC;③点P是△ACQ的外心;④![]() .其中正确的是______________(填序号)
.其中正确的是______________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC和BD相交于点O,正方形A1B1C1O的边OA1交AB于点E,OC1交BC于点F.
(1)求证:(BE+BF)2=2OB2;
(2)如果正方形ABCD的边长为a,那么正方形A1B1C1O绕O点转动的过程中,与正方形ABCD重叠部分的面积始终等于 (用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
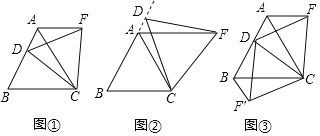
(1)操作发现:如图1,点D是等边△ABC边BA上一动点(点D与点B不重合),连结DC,以DC为边在CD上方作等边△DCF,连结AF,你能发现线段AF与BD之间的数量关系吗?证明你发现的结论.
(2)类比猜想:如图2,当动点D运动至等边△ABC边BA的延长线上时,其余条件不变,猜想:(1)中的结论是否成立,并说明理由.
(3)拓展探究:如图3.当动点D在等边△ABC边BA上运动时(点D与点B不重合),连结DC,以DC为边在CD上方和下方分别作等边△DCF和等边△DCF′,连结AF,BF′,探究:AF、BF′与AB有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
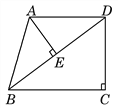
【题目】如图,已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AB,DC的延长线交于点E.
(1)求证:AC平分∠DAB;
(2)若BE=3,CE=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况,小卫在全校范围内随机抽取了若干名学生,就某日午饭浪费饭菜情况进行了调查.调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩余;D.饭和菜都有剩余.根据调查结果,绘制了如下两幅不完整的统计图.
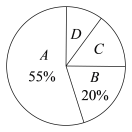
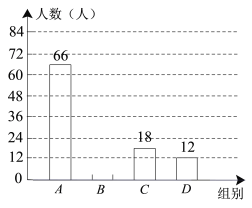
回答下列问题:
(1)扇形统计图中,“B组”所对应的圆心角的度数是_______;
(2)补全条形统计图;
(3)已知该中学共有学生2500人,请估计这日午饭有剩饭的学生人数;若按平均每人剩10克米饭计算,这日午饭将浪费多少千克米饭?.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com