
【题目】如图,正方形ABCD的对角线AC和BD相交于点O,正方形A1B1C1O的边OA1交AB于点E,OC1交BC于点F.
(1)求证:(BE+BF)2=2OB2;
(2)如果正方形ABCD的边长为a,那么正方形A1B1C1O绕O点转动的过程中,与正方形ABCD重叠部分的面积始终等于 (用含a的代数式表示)

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由题意得OA=OB,∠OAB=∠OBC=45°又因为∠AOE+∠EOB=90°,∠BOF+∠EOB=90°可得∠AOE=∠BOF,根据ASA可证△AOE≌△BOF,可得AE=BF,可得BE+BF=AB,由勾股定理可得结论;
(2)由全等三角形的性质可得S△AOE=S△BOF,可得重叠部分的面积为正方形面积的![]() ,即可求解.
,即可求解.
解:(1)在正方形ABCD中,AO=BO,∠AOB=90°,∠OAB=∠OBC=45°.
∵∠AOE+∠EOB=90°,∠BOF+∠EOB=90°,∴∠AOE=∠BOF.
在△AOE和△BOF中
 ,
,
∴△AOE≌△BOF(ASA),
∴AE=BF,
∴BE+EF=BE+AE=AB
在Rt△AOB中,AB2=OA2+OB2,且OA=OB,
∴(BE+BF)2=2OB2,
(2)∵△AOE≌△BOF,
∴S△AOE=S△BOF,
∴重叠部分的面积=S△AOB=![]() S正方形ABCD=
S正方形ABCD=![]() a2.
a2.
故答案为:![]() a2.
a2.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:

请根据上面的信息,解决问题:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上一点O为圆心,OB为半径作⊙O,交AC于点E,交AB于点D,且∠BEC=∠BDE.
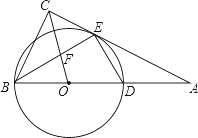
(1)求证:AC是⊙O的切线;
(2)连接OC交BE于点F,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OBCD中的三个顶点在⊙O上,点A是优弧BD上的一个动点(不与点B、D重合).
(1)当圆心O在∠BAD内部,∠ABO+∠ADO=50°时,∠A = °;
(2)当圆心O在∠BAD内部,四边形OBCD为平行四边形时,求∠C的度数;
(3)当圆心O在∠BAD外部,四边形OBCD为平行四边形时,请直接写出∠ABO与∠ADO的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军的爸爸和小慧的爸爸都是出租车司机,他们在每天的白天、夜间都要到同一加油站各加一次油.白天和夜间的油价不同,有时白天高,有时夜间高,但不管价格如何变化,他们两人采用固定的加油方式:小军的爸爸不论是白天还是夜间每次总是加![]() 油,小慧的爸爸则不论是白天还是夜间每次总是花
油,小慧的爸爸则不论是白天还是夜间每次总是花![]() 元钱加油.假设某天白天油的价格为每升
元钱加油.假设某天白天油的价格为每升![]() 元,夜间油的价格为每升
元,夜间油的价格为每升![]() 元.
元.
问:(1)小军的爸爸和小慧的爸爸在这天加油的平均单价各是多少?
(2)谁的加油方式更合算?请你通过数学运算,给以解释说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF.若∠EFD=15°,则∠CDF的度数为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com