
【题目】如果两个三角形两边和第三边上的中线对应成比例,那么这两个三角形相似.________(判断对错)
【答案】正确
【解析】
首先根据题意画出图形.已知,AD、A′D′分别是△ABC与△A′B′C′的中线,![]() .再作出辅助线倍长中线法:延长AD到M,使DM=AD,连结MC,证明△ABD≌△MCD,那么AB=MC,同理得出A′B′=M′C′,然后证明△ACM∽△A′C′M′,得出∠MAC=∠M′A′C′,同理可得∠MAB=∠M′A′B′,于是∠BAC=∠B′A′C′,再根据两边及其夹角法即可证明△ABC∽△A′B′C′.
.再作出辅助线倍长中线法:延长AD到M,使DM=AD,连结MC,证明△ABD≌△MCD,那么AB=MC,同理得出A′B′=M′C′,然后证明△ACM∽△A′C′M′,得出∠MAC=∠M′A′C′,同理可得∠MAB=∠M′A′B′,于是∠BAC=∠B′A′C′,再根据两边及其夹角法即可证明△ABC∽△A′B′C′.
正确.理由如下:
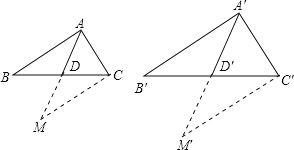
如图,AD、A′D′分别是△ABC与△A′B′C′的中线, ![]()
延长AD到M,使DM=AD,连结MC.
在△ABD与△MCD中,
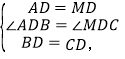
∴△ABD≌△MCD(SAS),
∴AB=MC,
同理延长A′D′到M′,使D′M′=A′D′,连结M′C′,那么A′B′=M′C′,
∴![]()
在△ACM与△A′C′M′中,
![]()
∴△ACM∽△A′C′M′,
∴∠MAC=∠M′A′C′,
同理可得∠MAB=∠M′A′B′,
∴∠MAC+∠MAB=∠M′A′C′+∠M′A′B′,∠BAC=∠B′A′C′.
在△ABC与△A′B′C′中,
![]()
∴△ABC∽△A′B′C′.
故答案为:正确.


科目:初中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AD∥BC,∠B=∠A=90°,AD=a,BC=b,AB=c,
操作示例
我们可以取直角梯形ABCD的一腰CD的中点P,过点P作PE∥AB,裁掉△PEC,并将△PEC拼接到△PFD的位置,构成新的图形(如图2).
思考发现
小明在操作后发现,该剪拼方法就是先将△PEC绕点P逆时针旋转180°到△PFD的位置,易知PE与PF在同一条直线上.又因为在梯形ABCD中,AD∥BC,∠C+∠ADP=180°,则∠FDP+∠ADP=180°,所以AD和DF在同一条直线上,那么构成的新图形是一个四边形,进而根据平行四边形的判定方法,可以判断出四边形ABEF是一个平行四边形,而且还是一个特殊的平行四边形——矩形.
1.图2中,矩形ABEF的面积是 ;(用含a,b,c的式子表示)
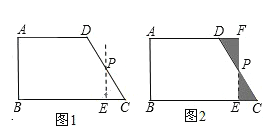
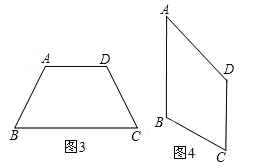
2.类比图2的剪拼方法,请你就图3(其中AD∥BC)和图4(其中AB∥DC)的两种情形分别画出剪拼成一个平行四边形的示意图.
3.小明通过探究后发现:在一个四边形中,只要有一组对边平行,就可以剪拼成平行四边形.
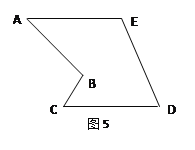
如图5的多边形中,AE=CD,AE∥CD,能否象上面剪切方法一样沿一条直线进行剪切,拼成一个平行四边形?若能,请你在图中画出剪拼的示意图并作必要的文字说明;若不能,简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
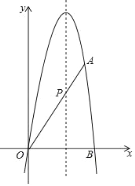
【题目】抛物线y=﹣![]() x2+bx+c(b,c均是常数)经过点O(0,0),A(4,4
x2+bx+c(b,c均是常数)经过点O(0,0),A(4,4![]() ),与x轴的另一交点为点B,且抛物线对称轴与线段OA交于点P.
),与x轴的另一交点为点B,且抛物线对称轴与线段OA交于点P.
(1)求该抛物线的解析式和顶点坐标;
(2)过点P作x轴的平行线l,若点Q是直线上的动点,连接QB.
①若点O关于直线QB的对称点为点C,当点C恰好在直线l上时,求点Q的坐标;
②若点O关于直线QB的对称点为点D,当线段AD的长最短时,求点Q的坐标(直接写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC和BD相交于点O,正方形A1B1C1O的边OA1交AB于点E,OC1交BC于点F.
(1)求证:(BE+BF)2=2OB2;
(2)如果正方形ABCD的边长为a,那么正方形A1B1C1O绕O点转动的过程中,与正方形ABCD重叠部分的面积始终等于 (用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
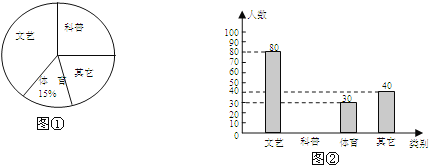
【题目】某校为了进一步丰富学生的课外阅读,欲增购一些课外书,为此对该校一部分学生进行了一次“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):
请根据图中提供的信息,完成下列问题:
(1)在这次问卷调查中,一共抽查了 名学生;并在图中补全条形统计图;
(2)如果全校共有学生1600名,请估计该校最喜欢“科普”书籍的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
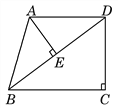
【题目】如图,已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于等腰三角形,有以下说法:
(1)有一个角为![]() 的等腰三角形一定是锐角三角形
的等腰三角形一定是锐角三角形
(2)等腰三角形两边的中线一定相等
(3)两个等腰三角形,若一腰以及该腰上的高对应相等,则这两个等腰三角形全等
(4)等腰三角形两底角的平分线的交点到三边距离相等
其中,正确说法的个数为( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
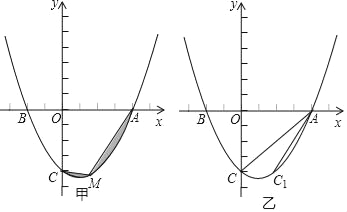
【题目】如图,已知抛物线过点A(4,0),B(﹣2,0),C(0,﹣4).
(1)求抛物线的解析式;
(2)在图甲中,点M是抛物线AC段上的一个动点,当图中阴影部分的面积最小值时,求点M的坐标;
(3)在图乙中,点C和点C1关于抛物线的对称轴对称,点P在抛物线上,且∠PAB=∠CAC1,求点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(![]() ,y2)是抛物线上两点,则
,y2)是抛物线上两点,则
y1>y2.其中说法正确的是( )
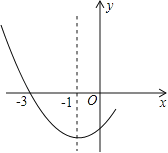
A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com