
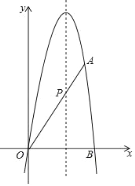
����Ŀ��������y=��![]() x2+bx+c��b��c���dz�����������O��0��0����A��4��4
x2+bx+c��b��c���dz�����������O��0��0����A��4��4![]() ������x�����һ����Ϊ��B���������߶Գ������߶�OA���ڵ�P��
������x�����һ����Ϊ��B���������߶Գ������߶�OA���ڵ�P��
��1����������ߵĽ���ʽ�Ͷ������ꣻ
��2������P��x���ƽ����l������Q��ֱ���ϵĶ��㣬����QB��
������O����ֱ��QB�ĶԳƵ�Ϊ��C������Cǡ����ֱ��l��ʱ�����Q�����ꣻ
������O����ֱ��QB�ĶԳƵ�Ϊ��D�����߶�AD�ij����ʱ�����Q�����ֱ꣨��д���𰸼��ɣ���
���𰸡���1��y=��![]() ��x��
��x��![]() ��2+
��2+![]() ����
����![]() ��
��![]() ������2��������
������2��������![]() ��
��![]() ����
����![]() ��
��![]() ��������0��
��������0��![]() ����
����
��������
1)��0(0,0),A(4,4v3)���������
y=��![]() x2+bx+c,ת��Ϊ�ⷽ���鼴��.
x2+bx+c,ת��Ϊ�ⷽ���鼴��.
(2)�����ֱ��OA�Ľ���ʽ,��B����,�����ߵĶԳ��ἴ�ɽ������.
(3)����ͼ1��,��O����ֱ��BQ�ĶԳƵ�Ϊ��C,����Cǡ����ֱ��l��ʱ,����֤���ı���BOQC������,��Q��m��![]() ��,����OQ=OB=5,�ɵ÷���
��,����OQ=OB=5,�ɵ÷���![]() ,�ⷽ�̼��ɽ������.
,�ⷽ�̼��ɽ������.
����ͼ2��,�������D����BΪԲ��5Ϊ�뾶��OB���˶�,��A,D��B����ʱ,�߶�AD��С,��OD��BQ���ڵ�H.�����D��H��������,�����ֱ��BH�Ľ���ʽ���ɽ������.
��1����O��0��0����A��4��4![]() �����������y=��
�����������y=��![]() x2+bx+c��
x2+bx+c��
��![]() ��
��
���![]() ��
��
�������ߵĽ���ʽΪy=��![]() x2+5
x2+5![]() x=��
x=��![]() ��x��
��x��![]() ��2+
��2+![]() ��
��
���������ߵĶ�������Ϊ��![]() ��
��![]() ����
����
��2����������B��5��0����A��4��4![]() ����
����
��ֱ��OA�Ľ���ʽΪy=![]() x��AB=
x��AB=![]() =7��
=7��
�������ߵĶԳ���x=![]() ��
��
��P��![]() ��
��![]() ����
����
��ͼ1�У���O����ֱ��BQ�ĶԳƵ�Ϊ��C������Cǡ����ֱ��l��ʱ��
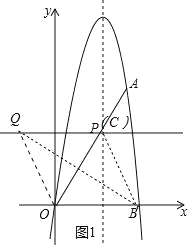
��QC��OB��
���CQB=��QBO=��QBC��
��CQ=BC=OB=5��
���ı���BOQC��ƽ���ı��Σ�
��BO=BC��
���ı���BOQC�����Σ�
��Q��m��![]() ����
����
��OQ=OB=5��
��m2+��![]() ��2=52��
��2=52��
��m=��![]() ��
��
���Q��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����
����ͼ2�У��������D����BΪԲ��5Ϊ�뾶�ġ�B���˶�����A��D��B����ʱ���߶�AD��С����OD��BQ���ڵ�H��
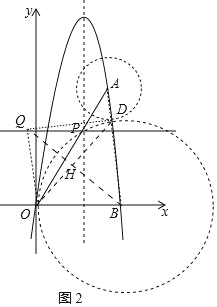
��AB=7��BD=5��
��AD=2��D��![]() ��
��![]() ����
����
��OH=HD��
��H��![]() ��
��![]() ����
����
��ֱ��BH�Ľ���ʽΪy=��![]() x+
x+![]() ��
��
��y=![]() ʱ��x=0��
ʱ��x=0��
��Q��0��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
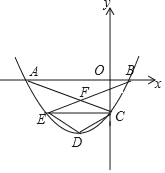
����Ŀ����ͼ��������y=mx2+2mx+n����A����3��0����C��0����![]() �����㣬��x�ύ����һ��B��
�����㣬��x�ύ����һ��B��
��1����A��B��C����������ߵĽ���ʽ��
��2������C��CE��x�ύ�������ڵ�E��д����E�����꣬����AC��BE�Ľ���F������
��3���������ߵĶ���ΪD������DC��DE���ı���CDEF�Ƿ�Ϊ���Σ����ǣ���֤���������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����![]() ��
��![]() (
(![]() �dz���,��
�dz���,��![]() )��ͬһƽ��ֱ������ϵ��ͼ������ǣ� ��
)��ͬһƽ��ֱ������ϵ��ͼ������ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ཫ���С���ѧ֪ʶ��������������С������Ʒ��������ͼ��С����ؽ�Ʒʱ���ĶԻ��龳��

������������Ϣ��������⣺
(1)�Լ������ֱʼDZ������˶��ٱ���
(2)������ͣ�С��Ϊʲô�������һ�68Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�һ���˽�ijУ����ѧ�������ʽ���״�������꼶�IJ���ѧ�����������ʼ�⣬ͬʱͳ����ÿ���˵ĵ÷�(��������÷�Ϊ![]() ������Ϊ50��).���ʼ��ijɼ���Ϊ�ĸ��ȼ�������
������Ϊ50��).���ʼ��ijɼ���Ϊ�ĸ��ȼ�������![]() ������
������![]() ���ϸ�
���ϸ�![]() �����ϸ�
�����ϸ�![]() �����ݵ���������������������������ͳ��ͼ���������ͳ��ͼ�ṩ����Ϣ�ش��������⣺
�����ݵ���������������������������ͳ��ͼ���������ͳ��ͼ�ṩ����Ϣ�ش��������⣺
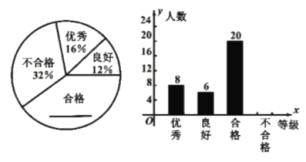
(1)��ȫ���������ͳ��ͼ������ͳ��ͼ��
(2)�����ԵIJ��ְ��꼶ѧ�������ʲ��Գɼ�����λ������ �ȼ�:
(3)����У���꼶��1400��ѧ�������Ƹ�У���꼶����Ϊ�����ϸ�����ѧ��Լ�ж�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=x2+bx+c�ĶԳ���Ϊx=2���ҹ���C��0��3��
��1����������ߵĽ���ʽ��
��2��֤�����������ߺ���ֱ��y=��2x+1�Ϸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90������б��AB��һ��OΪԲ�ģ�OBΪ�뾶����O����AC�ڵ�E����AB�ڵ�D���ҡ�BEC=��BDE��
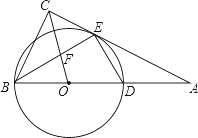
��1����֤��AC�ǡ�O�����ߣ�
��2������OC��BE�ڵ�F����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������ߺ͵������ϵ����߶�Ӧ�ɱ�������ô���������������ƣ�________���ж϶Դ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ijСѧ���ݽ�������ѡ���������У��ס��ҡ�����λ��ί��Сѡ�ֵ��ۺϱ��֣��ֱ������������������ĸW��ʾ������ͨ����������ĸP��ʾ���Ľ��ۣ�
��1��������״ͼ��ʾ����λ��ί��Сѡ�����������п��ܵĽ��ۣ�
��2������Сѡ��������ֻ�мס�����λ��ί������ͬ���۵ĸ����Ƕ��٣�
��3�������涨����λ��ί����������λ������ͨ�����Ľ��ۣ���Сѡ�ֿ���Χ���븴�������������븴���ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com