
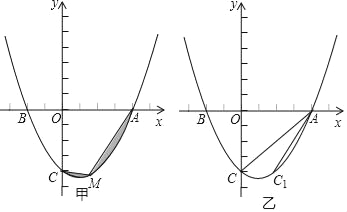
【题目】如图,已知抛物线过点A(4,0),B(﹣2,0),C(0,﹣4).
(1)求抛物线的解析式;
(2)在图甲中,点M是抛物线AC段上的一个动点,当图中阴影部分的面积最小值时,求点M的坐标;
(3)在图乙中,点C和点C1关于抛物线的对称轴对称,点P在抛物线上,且∠PAB=∠CAC1,求点P的横坐标.
【答案】(1)y=![]() x2-x-4(2)点M的坐标为(2,-4)(3)-
x2-x-4(2)点M的坐标为(2,-4)(3)-![]() 或-
或-![]()
【解析】
(1)设交点式y=a(x+2)(x-4),然后把C点坐标代入求出a即可得到抛物线解析式;
(2) 连接OM,设点M的坐标为![]() .由题意知,当四边形OAMC面积最大时,阴影部分的面积最小.S四边形OAMC=S△OAM+S△OCM-(m-2)2+12. 当m=2时,四边形OAMC面积最大,此时阴影部分面积最小;
.由题意知,当四边形OAMC面积最大时,阴影部分的面积最小.S四边形OAMC=S△OAM+S△OCM-(m-2)2+12. 当m=2时,四边形OAMC面积最大,此时阴影部分面积最小;
(3) 抛物线的对称轴为直线x=1,点C与点C1关于抛物线的对称轴对称,所以C1(2,-4).连接CC1,过C1作C1D⊥AC于D,则CC1=2.先求AC=4![]() ,CD=C1D=
,CD=C1D=![]() ,AD=4
,AD=4![]() -
-![]() =3
=3![]() ;设点P
;设点P![]() ,过P作PQ垂直于x轴,垂足为Q. 证△PAQ∽△C1AD,得
,过P作PQ垂直于x轴,垂足为Q. 证△PAQ∽△C1AD,得![]() ,即
,即![]() ,解得解得n=-
,解得解得n=-![]() ,或n=-
,或n=-![]() ,或n=4(舍去).
,或n=4(舍去).
(1)抛物线的解析式为y=![]() (x-4)(x+2)=
(x-4)(x+2)=![]() x2-x-4.
x2-x-4.
(2)连接OM,设点M的坐标为![]() .
.
由题意知,当四边形OAMC面积最大时,阴影部分的面积最小.
S四边形OAMC=S△OAM+S△OCM
=![]() × 4m+
× 4m+![]() × 4
× 4![]()
=-m2+4m+8=-(m-2)2+12.
当m=2时,四边形OAMC面积最大,此时阴影部分面积最小,所以点M的坐标为(2,-4).
(3)∵抛物线的对称轴为直线x=1,点C与点C1关于抛物线的对称轴对称,所以C1(2,-4).
∵OA=OC,∠AOC=90°,∠CDC1=90°,
∴AC=4![]() ,CD=C1D=
,CD=C1D=![]() ,AD=4
,AD=4![]() -
-![]() =3
=3![]() ,
,
设点P![]() ,过P作PQ垂直于x轴,垂足为Q.
,过P作PQ垂直于x轴,垂足为Q.
∵∠PAB=∠CAC1,∠AQP=∠ADC1,
∴△PAQ∽△C1AD,
∴![]() ,
,
即![]() ,化简得
,化简得![]() =(8-2n),
=(8-2n),
即3n2-6n-24=8-2n,或3n2-6n-24=-(8-2n),
解得n=-![]() ,或n=-
,或n=-![]() ,或n=4(舍去),
,或n=4(舍去),
∴点P的横坐标为-![]() 或-
或-![]() .
.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:

请根据上面的信息,解决问题:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军的爸爸和小慧的爸爸都是出租车司机,他们在每天的白天、夜间都要到同一加油站各加一次油.白天和夜间的油价不同,有时白天高,有时夜间高,但不管价格如何变化,他们两人采用固定的加油方式:小军的爸爸不论是白天还是夜间每次总是加![]() 油,小慧的爸爸则不论是白天还是夜间每次总是花
油,小慧的爸爸则不论是白天还是夜间每次总是花![]() 元钱加油.假设某天白天油的价格为每升
元钱加油.假设某天白天油的价格为每升![]() 元,夜间油的价格为每升
元,夜间油的价格为每升![]() 元.
元.
问:(1)小军的爸爸和小慧的爸爸在这天加油的平均单价各是多少?
(2)谁的加油方式更合算?请你通过数学运算,给以解释说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
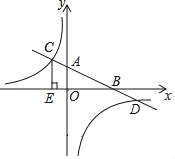
【题目】已知:如图,在平面直角坐标系xOy中,直线AB分别与x轴、y轴交于点B,A,与反比例函数的图象分别交于点C,D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求该反比例函数的解析式;
(2)求三角形CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
商店经营有A、B两种品牌的笔,A种笔的单价比B种笔的单价贵2元,若花140买A种笔,120元买B种笔,则A种笔反而比B种笔少一支.
(1)求A、B两种品牌的笔每支各多少元.
(2)某单位准备一次性购买两种笔共200支,预计费用不超过1800元.并且规定,A种笔的数量不能少于B种笔的![]() .问如何购买,单位花钱最少?最少花多少钱?
.问如何购买,单位花钱最少?最少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某小学“演讲大赛”选拔赛初赛中,甲、乙、丙三位评委对小选手的综合表现,分别给出“待定”(用字母W表示)或“通过”(用字母P表示)的结论.
(1)请用树状图表示出三位评委给小选手琪琪的所有可能的结论;
(2)对于小选手琪琪,只有甲、乙两位评委给出相同结论的概率是多少?
(3)比赛规定,三位评委中至少有两位给出“通过”的结论,则小选手可入围进入复赛,问琪琪进入复赛的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF.若∠EFD=15°,则∠CDF的度数为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应香洲区全面推进书香校园建设的号召,班长小青随机调查了若干同学一周课外阅读的时间t(单位:小时),将获得的数据分成四组,绘制了如下统计图(A:0<t≤7,B:7<t≤14,C:14<t≤21,D:t>21),根据图中信息,解答下列问题:

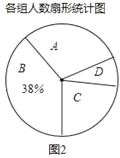
(1)这项工作中被调查的总人数是多少?
(2)补全条形统计图,并求出表示A组的扇形统计图的圆心角的度数;
(3)如果小青想从D组的甲、乙、丙、丁四人中先后随机选择两人做读书心得发言代表,请用列表或树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com