
分析 A、分类讨论:当点E在线段AE上,如图1,根据菱形的性质得BC=AD=8,BC∥AD,则AE=5,利用BC∥AM,根据平行线分线段成比例定理得到$\frac{MC}{AM}$=$\frac{BC}{AE}$=$\frac{8}{5}$;当点E在线段AE的延长线上,如图2,则AE=11,同理可得$\frac{MC}{AM}$=$\frac{8}{11}$;
B、直接使用科学计算器进行计算.
解答 解:A、当点E在线段AE上,如图1,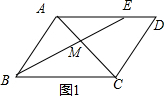
∵菱形ABCD的边长是8,
∴BC=AD=8,BC∥AD,
∵DE=3,
∴AE=5,
∵BC∥AM,
∴$\frac{MC}{AM}$=$\frac{BC}{AE}$=$\frac{8}{5}$;
当点E在线段AE的延长线上,如图2,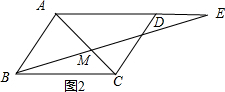 则AE=11,
则AE=11,
∵BC∥AM,
∴$\frac{MC}{AM}$=$\frac{BC}{AE}$=$\frac{8}{11}$,
即$\frac{MC}{AM}$的值为$\frac{8}{5}$或$\frac{8}{11}$;
B、$\sqrt{7}$sin69°≈2.47(精确到0.01).
故答案为$\frac{8}{5}$或$\frac{8}{11}$; 2.47.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了平行线分线段成比例定理和计算器的使用.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
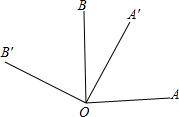 如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.
如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com