
【题目】为了参加“仙桃市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(l)班 86,85,77,92,85;八(2)班 79,85,92,85,89.通过数据分析,列表如下:
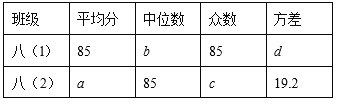
(1)直接写出表中a,b,c,d的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
【答案】(1)a=86,b=85,c=85,d=22.8;(2) 八(2)班前5名同学的成绩较好,理由见解析
【解析】
(1)根据平均数、中位数、众数的概念解答, 根据方差计算公式,求出八(1)班的方差即可;
(2)先根据方差计算公式,求出八(1)班的方差,结合平均数、中位数、众数与方差的意义求解即可;
(1)八(2)班的平均分a=(79+85+92+85+89)÷5=86,
将八(1)班的前5名学生的成绩按从小到大的顺序排列为:77,85,85,86,92,第三个数是85,所以中位数b=85,
85出现了2次,次数最多,所以众数c=85.
八(1)班的方差d=[(86-85)2+(85-85)2+(77-85)2+(92-85)2+(85-85)2]÷5=22.8;
故答案为86,85,85,22.8;
(2)∵由数据可知,两班成绩中位数,众数相同,而八(2)班平均成绩更高,且方差更小,成绩更稳定,
∴八(2)班前5名同学的成绩较好;


科目:初中数学 来源: 题型:
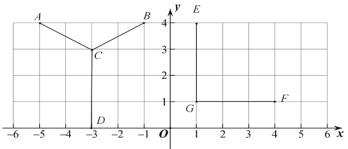
【题目】(1)写出点![]() 的坐标
的坐标
(2)线段![]() 先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段
先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段![]() 重合.
重合.
(3)已知在![]() 轴上存在点
轴上存在点![]() 与
与![]() 围成的三角形面积为6,请写出
围成的三角形面积为6,请写出![]() 的坐标
的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是考古学家发现的古代钱币的一部分,合肥一中的小明正好学习了圆的知识,他想求其外圆半径,连接外圆上的两点A,B,并使AB与内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10 cm,AB=60 cm,则这个钱币的外圆半径为__cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下述材料:
下述形式的繁分数叫做有限连分数,其中n是自然数,a0是整数,a1,a2,a3,…,an是正整数:

其中![]() 称为部分商。
称为部分商。
按照以下方式可将任何一个分数转化为连分数的形式:![]() ,则
,则![]() ;考虑
;考虑![]() 的倒数,有
的倒数,有![]() ,从而
,从而 ;再考虑
;再考虑![]() 的倒数,有
的倒数,有![]() ,于是得到a的连分数展开式,它有4个部分商:3,1,3,3;
,于是得到a的连分数展开式,它有4个部分商:3,1,3,3;

可利用连分数来求二元一次不定方程的特殊解,以![]() 为例,首先将
为例,首先将![]() 写成连分数的形式,如上所示;其次,数部分商的个数,本例是偶数个部分商(奇数情况请见下例);最后计算倒数第二个渐近分数
写成连分数的形式,如上所示;其次,数部分商的个数,本例是偶数个部分商(奇数情况请见下例);最后计算倒数第二个渐近分数 ,从而
,从而![]() 是一个特解。
是一个特解。
考虑不定方程![]() ,先将
,先将![]() 写成连分数的形式:
写成连分数的形式: 。
。
注意到此连分数有奇数个部分商,将之改写为偶数个部分商的形式:

计算倒数第二个渐近分数: ,所以
,所以![]() 是
是![]() 的一个特解。
的一个特解。
对于分式,有类似的连分式的概念,利用将分数展开为连分数的方法,可以将分式展开为连分式。例如![]() 的连分式展开式如下,它有3个部分商:
的连分式展开式如下,它有3个部分商:![]()
![]() ;
;

再例如, ,它有4个部分商:1,
,它有4个部分商:1,![]() 。
。
请阅读上述材料,利用所讲述的方法,解决下述两个问题
(1)找出两个关于x的多项式p和q,使得![]() 。
。
(2)找出两个关于x的多项式u和v,使得![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
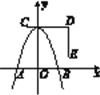
【题目】如图,一条抛物线与x轴相交于A,B两点,其顶点P在折线C-D-E上移动,若点C,D,E的坐标分别为(-1,4),(3,4),(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,已知数
,已知数![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() .
.
![]()
(1)![]() ,
,![]() ,
,![]() ;
;
(2)若将数轴折叠,使得点![]() 与点
与点![]() 重合,则点
重合,则点![]() 与数 表示的点重合;
与数 表示的点重合;
(3)点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒2个单位长度和4个单位长度的速度向右运动,假设
分别以每秒2个单位长度和4个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,求
,求![]() 、
、![]() 、
、![]() 的长(用含
的长(用含![]() 的式子表示);
的式子表示);
(4)在(3)的条件下,![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若改变,请说明理由;若不变,请求其值.
的变化而改变?若改变,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某街区的平面示意图,根据要求答题.

(1)这幅图的比例尺是( )
(2)学校位于广场的( )面(填东、南、西、北)( )千米处.
(3)人民公园位于广场的东偏南![]() 方向3千米处.在图中标出它的位置.
方向3千米处.在图中标出它的位置.
(4)广场的西面1千米处,有一条商业街与人民路垂直,在图中画线表示商业街.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0.
(1)判断方程根的情况;
(2)若方程的两根x1,x2满足(x1-1)(x2-1)=5,求k值;
(3)若△ABC的两边AB,AC的长是方程的两根,第三边BC的长为5,
①则k为何值时,△ABC是以BC为斜边的直角三角形?
②k为何值时,△ABC是等腰三角形,并求出△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com