
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG. 
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.
【答案】
(1)证明:∵BE⊥AC,CF⊥AB,
∴∠HFB=∠HEC=90°,又∵∠BHF=∠CHE,
∴∠ABD=∠ACG,
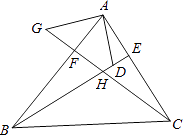
在△ABD和△GCA中
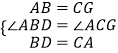 ,
,
∴△ABD≌△GCA(SAS),
∴AD=GA(全等三角形的对应边相等)
(2)证明:位置关系是AD⊥GA,
理由为:∵△ABD≌△GCA,
∴∠ADB=∠GAC,
又∵∠ADB=∠AED+∠DAE,∠GAC=∠GAD+∠DAE,
∴∠AED=∠GAD=90°,
∴AD⊥GA.
【解析】(1)由BE垂直于AC,CF垂直于AB,利用垂直的定义得∠HFB=∠HEC,由得对顶角相等得∠BHF=∠CHE,所以∠ABD=∠ACG.再由AB=CG,BD=AC,利用SAS可得出三角形ABD与三角形ACG全等,由全等三角形的对应边相等可得出AD=AG,(2)利用全等得出∠ADB=∠GAC,再利用三角形的外角和定理得到∠ADB=∠AED+∠DAE,又∠GAC=∠GAD+∠DAE,利用等量代换可得出∠AED=∠GAD=90°,即AG与AD垂直.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线C1:![]() 和C2:
和C2:![]() 都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是 和 .
都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是 和 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表

我们把某格中字母和所得的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
(1)第3格的“特征多项式”为 ,第4格的“特征多项式”为 ,第n格的“特征多项式”为 ;
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16,求x,y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com