
【题目】为了弘扬优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“两个黄鹂鸣翠柳”.
(1)小明回答该问题时,对第二个字是选“个”还是选“只”难以抉择,若随机选择其中一个,则小明回答正确的概率是__________;
(2)小丽回答该问题时,对第二个字是选“个”还是选“只”、第五个字是选“鸣”还是选“明”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3).

(1)请画出△ABC关于y轴对称的△DEF(其中D、E、F分别是A、B、C的对应点).
(2)直接写出(1)中F点的坐标为 .
(3)若直线l经过点(0,﹣2)且与x轴平行,则点C关于直线l的对称点的坐标为 .
(4)在y轴上存在一点P,使PC﹣PB最大,则点P的坐标为 .
(5)第一象限有一点M(4,2),在x轴上找一点Q使CQ+MQ最短,画出最短路径,保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=﹣2x2+4x+m+1,与x轴的公共点为A,B.
(1)如果A与B重合,求m的值;
(2)横、纵坐标都是整数的点叫做整点:
①当m=﹣1时,求线段AB上整点的个数;
②若设抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,当1<n≤8时,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.

(1)当点E为AB的中点时(如图1),则有AE DB(填“>”“<”或“=”);
(2)猜想AE与DB的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.

理解:
⑴如图![]() ,已知
,已知![]() 是⊙
是⊙![]() 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点![]() ,使
,使![]() 为“智慧三角形”(画出点
为“智慧三角形”(画出点![]() 的位置,保留作图痕迹);
的位置,保留作图痕迹);
⑵如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;
运用:
⑶如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,⊙
中,⊙![]() 的半径为
的半径为![]() ,点
,点![]() 是直线
是直线![]() 上的一点,若在⊙
上的一点,若在⊙![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为“智慧三角形”,当其面积取得最小值时,直接写出此时点
为“智慧三角形”,当其面积取得最小值时,直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两家运输公司规定每位旅客携带行李的费用与所带行李质量之间的关系图.
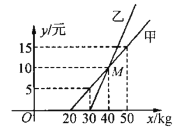
(1)由图可知,行李质量只要不超过______kg,甲公司就可免费携带,如果超过了规定的质量,则每超过1 kg要付运费_______元;
(2)若设旅客携带的行李质量为x(kg),所付的行李费是y(元),请分别写出y甲与y乙(元)随x(kg)之间变化的关系式;
(3)若你准备携带45 kg的行李出行,在甲、乙两家公司中你会选择哪一家?应付行李费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是菱形
是菱形![]() 的对角线
的对角线![]() 、
、![]() 的交点,
的交点,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.下列结论:①
的中点.下列结论:①![]() ;②四边形
;②四边形![]() 也是菱形;③四边形
也是菱形;③四边形![]() 的面积为
的面积为![]() ;④
;④![]() ;⑤
;⑤![]() 是轴对称图形.其中正确的结论有( )
是轴对称图形.其中正确的结论有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵BE=AB,∴AE=2AB.
∵AD=2AB,∴AD=AE.
∵四边形ABCD是矩形,∴AD∥BC.
∴![]() .(依据1)
.(依据1)
∵BE=AB,∴![]() .∴EM=DM.
.∴EM=DM.
即AM是△ADE的DE边上的中线,
又∵AD=AE,∴AM⊥DE.(依据2)
∴AM垂直平分DE.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C,点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com