
【题目】如图,直线y=kx与双曲线y=﹣![]() 交于A(x1,y1),B(x2,y2)两点,则2x1y2﹣8x2y1的值为( )
交于A(x1,y1),B(x2,y2)两点,则2x1y2﹣8x2y1的值为( )
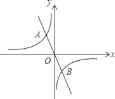
A. ﹣6 B. ﹣12 C. 6 D. 12
【答案】B
【解析】
(解法一)将一次函数解析式代入反比例函数解析式中得出关于x的一元二次方程,解方程即可得出A、B点的横坐标,再结合一次函数的解析式即可求出点A、B的坐标,将其代入2x1y2-8x2y1中即可得出结论.
(解法二)根据正、反比例函数的对称性,找出x1=-x2、y1=-y2,将其代入2x1y2-8x2y1中利用反比例函数图象上点的坐标特征,即可求出结论.
(解法一)将y=kx代入到y=-![]() 中得:
中得:
kx=-![]() ,即kx2=-2,
,即kx2=-2,
解得:x1=-![]() ,x2=
,x2=![]() ,
,
∴y1=kx1=![]() ,y2=kx2=-
,y2=kx2=-![]() ,
,
∴2x1y2-8x2y1=2×(-![]() )×(-
)×(-![]() )-8×
)-8×![]() ×
×![]() =-12.
=-12.
(解法二)由正、反比例函数的对称性,可知:x1=-x2,y1=-y2,
∴2x1y2-8x2y1=-2x1y1+8x1y1=6x1y1.
∵x1y1=-2,
∴2x1y2-8x2y1=6x1y1=-12.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x-m)2-2a(x-m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,当△ABC是等腰直角三角形时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体院要了解篮球专业学生投篮的命中率,对学生进行定点投篮测试,规定每人投篮20次,测试结束后随机抽查了一部分学生投中的次数,并分为五类,Ⅰ:投中11次;Ⅱ投中12次;Ⅲ:投中13次;Ⅳ:投中14次;Ⅴ:投中15次.根据调查结果绘制了下面尚不完整的统计图1、图2: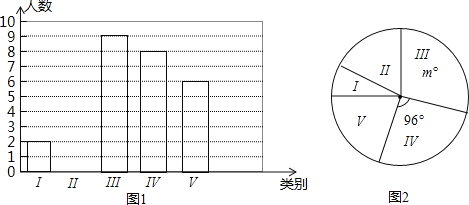
回答下列问题:
(1)本次抽查了 名学生,图2中的m= .
(2)补全条形统计图,并指出中位数在哪一类.
(3)求最高的命中率及命中最高的人数所占的百分比.
(4)若体院规定篮球专业学生定点投篮命中率不低于65%记作合格,估计该院篮球专业210名学生中约有多少人不合格.
查看答案和解析>>
科目:初中数学 来源: 题型:
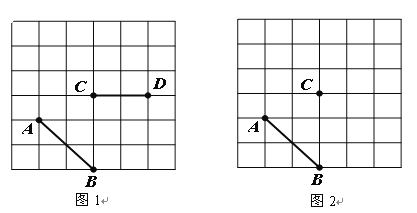
【题目】如图,正方形网格中,小格的顶点叫做格点,连接任意两个格点的线段叫做格点线段。
(1)如图1,格点线段AB、CD,请添加一条格点线段EF,使它们构成轴对称图形;
(2)如图2,格点线段AB和格点C,在网格中找一格点D,使格点A、B、C、D四点构成中心对称图形;
(3)在(2)的条件下,如果每一小正方形边长为1,那么四边形ABCD的面积S为_________.
(请直接填写)
查看答案和解析>>
科目:初中数学 来源: 题型:
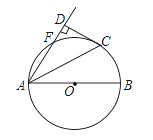
【题目】如图,AB是⊙O的直径,点F、C在⊙O上且![]() , 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
, 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
(1)求证:CD是⊙O的切线;
(2)若![]() , CD=4,求⊙O的半径.
, CD=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
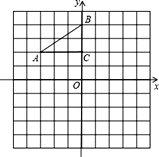
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,在建立直角坐标系后,点C的坐标(-1,2)
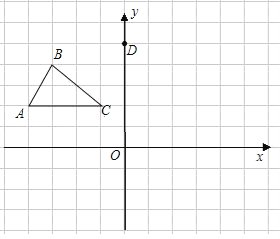
(1)画出△ABC绕点D(0,5)逆时针旋转90°后的△A1B1C1,
(2)写出A1,C1的坐标.
(3)求点A旋转到A1所经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
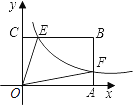
【题目】如图,已知双曲线 ![]() (x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE=
(x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE= ![]() CB,AF=
CB,AF= ![]() AB,且四边形OEBF的面积为2,则k的值为________.
AB,且四边形OEBF的面积为2,则k的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com