不等式2x+1＜3的解集在数轴上表示为( )A．B．C．D．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

15．不等式2x+1＜3的解集在数轴上表示为（　　）

A．

B．

C．

D．

分析根据不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），可得答案．

解答解：2x+1＜3，
解得x＜1，
在数轴上表示为：

故选：D．

点评本题考查了在数轴上表示不等式的解集，不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），注意在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

5．x为何值时，$\frac{x}{x-1}$在实数范围内有意义（　　）

A．

x＞1

B．

x≥1

C．

x≠1

D．

x≤0

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

6．

一个正方体的展开图如图所示，将它折成正方体后，数字“0”的对面是（　　）

A．

数

B．

C．

D．

学

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

3．吉林省交警总队公布的数据显示，截止到2015年9月1日，全省机动车保有量超过4530000辆，4530000这个数用科学记数法表示为（　　）

A．

0.453×10⁷

B．

4.53×10⁶

C．

4.53×10⁷

D．

45.3×10⁵

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

10．

如图，在平面直角坐标系中，直线y=-x+1上一点A关于x轴的对称点为B（2，m），则m的值为（　　）

A．

-1

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

20．一元二次方程x²-3x-1=0根的判别式△=13．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．

阅读材料
通过前面的学习我们已经知道了两点之间的距离，点到直线的距离和两条平行线间的距离，那么我们如何在平面直角坐标系中求这些距离呢？
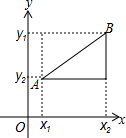
如图1，在平面直角坐标系xOy中，A、B两点的坐标分为A（x₁，y₁），B（x₂，y₂），由勾股定理得AB₂=|x₁-x₂|²+|y₁-y₂|²，所以A、B两点间的距离为AB=$\sqrt{|{x}_{1}-{x}_{2}{|}^{2}+|{y}_{1}-{y}_{2}{|}^{2}}$．这样就可以求出平面直角坐标系中任意两点间的距离．
我们用下面的公式可以求出平面直角坐标系中任意一点到某条直线的距离：
已知点P（x₀，y₀）和直线y=kx+b，则点P到直线y=kx+b的距离d可用公式d=$\frac{|k{x}_{0}-{y}_{0}+b|}{\sqrt{1+{k}^{2}}}$
计算：例如：求点P（-2，1）到直线y=x+1的距离．
解：因为直线y=x+1可变形为x-y+1=0，其中k=1，b=1．
所以点P（-2，1）到直线y=x+1的距离了为d=$\frac{|k{x}_{0}-{y}_{0}+b|}{\sqrt{1+{k}^{2}}}$=$\frac{|1×（-2）-1+1|}{\sqrt{1+{1}^{2}}}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$．
根据以上材料，解决下列问题：
（1）已知A（-2，1），B（4，3），求线段AB的长度；
（2）点P（1，1）到直线y=3x-2的距离，并说明点P与直线的位置关系；
（3）点P（2，-1）到直线y=2x-1的距离；
（4）已知直线y=-x+1与y=-x+3平行，求这两条直线的距离．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

4．

如图，BA⊥FC于A点，过A点作DE∥BC，若∠EAF=125°，则∠B=35°．