
Ϊ�˹��������Լ��ˮ��ij�в��á�����ˮ�ۡ��ķ������¼���ÿ����ͥ��ˮ�ѣ�ÿ����ˮ��������20��ʱ����ÿ��2Ԫ�Ʒѣ�ÿ����ˮ������20��ʱ�����е�20����ÿ��2Ԫ�Ʒѣ��������ְ�ÿ��2.8Ԫ�Ʒѣ���ÿ����ͥÿ����ˮ��Ϊx��ʱ��Ӧ��ˮ��yԪ��
��1���ֱ����0��x��20��x��20ʱ��y��x֮��ĺ�������ʽ��
��2��Сӱ�����·ݡ����·ݷֱ�ˮ��45.6Ԫ��38Ԫ����Сӱ�����·ݱ����·ݽ�Լ��ˮ���ٶ֣�
��1����0��x��20ʱ�� y=2x����x��20ʱ�� y==2.8x-16����2��3.
��������
�����������1����Ϊ����ˮ��������20��ʱ����2Ԫ/�ּƷѣ����Ե�0��x��20ʱ��y��x�ĺ�������ʽ��y=2x����Ϊ����ˮ������20��ʱ�����е�20����2Ԫ/���շѣ��������ְ�2.8Ԫ/�ּƷѣ����Ե�x��20ʱ��y��x�ĺ�������ʽ��y=2��20+2.8��x-20������y=2.6x-12��
��2��������ɵã���Ϊ���·ݽɷѽ�����40Ԫ��������y=2x������ˮ�������·ݽɷѽ���40Ԫ��������y=2.8x-16������ˮ������һ���ó�������ɣ�
�����������1����0��x��20ʱ��y��x�ĺ�������ʽ��y=2x��
��x��20ʱ��y��x�ĺ�������ʽ��y=2��20+2.8��x-20��=2.8x-16��
��2����ΪСӱ�����·ݵ�ˮ�Ѷ�������40Ԫ�����·ݵ�ˮ�ѳ���40Ԫ��
����y=38����y=2x����x=19��
��y=45.6����y=2.8x-16����x=22��
����22-19=3�֣�
��Сӱ�����·ݱ����·ݽ�Լ��ˮ3�֣�
�����㡿һ�κ�����Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ���������ˮ������ѧ�������棩 ���ͣ������
��ͼ��һ�κ���y1=k1x+b��k1��0����ͼ���뷴��������y2=k2x+b��k2��0����ͼ����A��B���㣬�۲�ͼ��y1��y2ʱ��x��ȡֵ��Χ���� ����
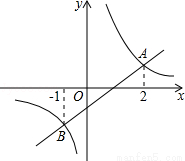
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�������ƽ������ѧ�������棩 ���ͣ������
��ͼ1��ͼ2��ͼ3��ͼ4�У���P���߶�BC���ƶ�������B��C�غϣ���M��BC���ӳ����ϣ�
��1����ͼ1����ABC����APE��Ϊ�������Σ�����CE��
����֤����ABP�ա�ACE��
�ڡ�ECM�Ķ���Ϊ�� ���㣮
��2������ͼ2�����ı���ABCD���ı���APEF��Ϊ�����Σ�����CE������ECM�Ķ���Ϊ�� ���㣮
����ͼ3���������ABCDF�������APEGH��Ϊ������Σ�����CE������ECM�Ķ���Ϊ�� ���㣮
��3����ͼ4��n����ABC����n����APE����Ϊ��n���Σ�����CE������̽����������ECM�Ķ�����������α���n��������ϵ���ú�n��ʽ�ӱ�ʾ��ECM�Ķ�������������ͼ4���Ŵ��ľֲ�ͼ�Σ�֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�������ƽ������ѧ�������棩 ���ͣ�ѡ����
��ͼ����ABC�У�AD��BE���������ߣ���S��EDC��S��ABC=��������
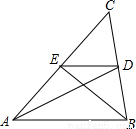
A��1��2 B��2��3 C��1��3 D��1��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�������ƽ������ѧ�������棩 ���ͣ�ѡ����
��ͼ�������������ͼ�ǣ�������

A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ���������������ѧ�������棩 ���ͣ������
�ⲻ��ʽ2��x-2����1-3x���������Ľ⼯�������ϱ�ʾ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ���������������ѧ�������棩 ���ͣ�ѡ����
��֪���κ���y=-x2+2bx+c����x��1ʱ��y��ֵ��xֵ���������С����ʵ��b��ȡֵ��Χ�ǣ�������
A��b��-1 B��b��-1 C��b��1 D��b��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�������ˮ������ѧ�������棩 ���ͣ������
���ݵ�·�����涨�����˻ʴ�����������������ʻ�ij���������60ǧ��/ʱ����֪����վ��M���˻ʴ��l��ֱ�ߣ��ľ���MNΪ30�ף���ͼ��ʾ��������һ���������������������������ʻ����ô˳���A����ʻ��B������ʱ��Ϊ6�룬��AMN=60������BMN=45����
��1������AB�ij��ȣ�
��2��ͨ�������жϴ˳��Ƿ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������ݾ�����ѧ�������棩 ���ͣ�ѡ����
������y=��x��1��2��3�ĶԳ����ǣ�������
A��y�� B��ֱ��x=��1 C��ֱ��x=1 D��ֱ��x=��3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com