Question

在图1、图2、图3、图4中，点P在线段BC上移动（不与B、C重合），M在BC的延长线上．

（1）如图1，△ABC和△APE均为正三角形，连接CE．

①求证：△ABP≌△ACE．

②∠ECM的度数为　 　°．

（2）①如图2，若四边形ABCD和四边形APEF均为正方形，连接CE．则∠ECM的度数为　 　°．

②如图3，若五边形ABCDF和五边形APEGH均为正五边形，连接CE．则∠ECM的度数为　 　°．

（3）如图4，n边形ABC…和n边形APE…均为正n边形，连接CE，请你探索并猜想∠ECM的度数与正多边形边数n的数量关系（用含n的式子表示∠ECM的度数），并利用图4（放大后的局部图形）证明你的结论．

 

 

Answer 1

(1)60；（2）45，36．（3）.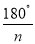

【解析】

试题分析：（1）①由△ABC与△APE均为正三角形得出相等的角与边，即可得出△ABP≌△ACE．

②由△ABP≌△ACE，得出∠ACE=∠B=60°，即可得出∠ECM的度数．

（2）①作EN⊥BN，交BM于点N，由△ABP≌△ACE，利用角及边的关系，得出CN=EN，即可得出∠ECM的度数．

②作EN⊥BN，交BM于点N，由△ABP≌△ACE，得出角及边的关系，得出CN=EN，即可得出∠ECM的度数．

（3）过E作EK∥CD，交BM于点K，由正多边形的性质可得出△ABP≌△PKE，利用角及边的关系，得出CK=KE，即△EKC是等腰三角形，根据多边形的内角即可求出∠ECM的度数．[来

试题解析：（1）①证明：如图1，

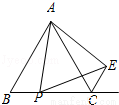
∵△ABC与△APE均为正三角形，

∴AB=AC，AP=AE，∠BAC=∠PAE=60°，

∴∠BAC-∠PAC=∠PAE-∠PAC

即∠BAP=∠CAE，

在△ABP和△ACE中，

，

∴△ABP≌△ACE （SAS）．

②∵△ABP≌△ACE，

∴∠ACE=∠B=60°，

∵∠ACB=60°，

∠ECM=180°-60°-60°=60°．

（2）①如图2，作EN⊥BN，交BM于点N

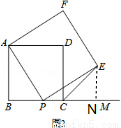
∵四边形ABCD和APEF均为正方形，

∴AP=PE，∠B=∠ENP=90°，

∴∠BAP+∠APB=∠EPM+∠APB=90°，

即∠BAP=∠NPE，

在△ABP和△PNE中，

，

∴△ABP≌△ACE （AAS）．

∴AB=PN，BP=EN，

∵BP+PC=PC+CN=AB，

∴BP=CN，

∴CN=EN，

∴∠ECM=∠CEN=45°

②如图3，作EN∥CD交BM于点N，

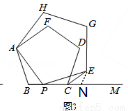
∵五边形ABCDF和APEGH均为正五边方形，

∴AP=PE，∠B=∠BCD，

∵EN∥CD，

∴∠PNE=∠BCD，

∴∠B=∠PNE

∵∠BAP+∠APB=∠EPM+∠APB=180°-∠B，

即∠BAP=∠NPE，

在△ABP和△PNE中，

，

∴△ABP≌△ACE （AAS）．

∴AB=PN，BP=EN，

∵BP+PC=PC+CN=AB，

∴BP=CN，

∴CN=EN，

∴∠NCE=∠NEC，

∵∠CNE=∠BCD=108°，

∴∠ECM=∠CEN=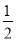（180°-∠CNE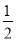）=×（180°-108°）=36°．

（3）如图4中，过E作EK∥CD，交BM于点K，

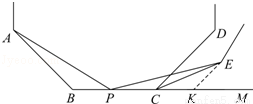
∵n边形ABC…和n边形APE…为正n边形，

∴AB=BC AP=PE

∠ABC=∠BCD=∠APE=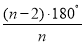

∵∠APK=∠ABC+∠BAP，∠APK=∠APE+∠EPK

∴∠BAP=∠KPE

∵EK∥CD，

∴∠BCD=∠PKE

∴∠ABP=∠PKE，

在△ABP和△PKE中，

，

∴△ABP≌△PKE（AAS）

∴BP=EK，AB=PK，

∴BC=PK，

∴BC-PC=PK-PC，

∴BP=CK，

∴CK=KE，

∴∠KCE=∠KEC，

∵∠CKE=∠BCD=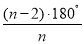

∴∠ECK=．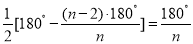

考点：四边形综合题．