练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    2014年12月26日，西南真正意义上的第一条高铁﹣贵阳至广州高速铁路将开始试运行，从贵阳到广州，乘特快列车的行程约为1800km，高铁开通后，高铁列车的行程约为860km，运行时间比特快列车所用的时间减少了16h．若高铁列车的平均速度是特快列车平均速度的2．5倍，求特快列车的平均速度．

     

    91km/h．

    【解析】

    试题分析：方程的应用解题关键是设出未知数，找出关键描述语，确定等量关系，列出方程求解．本题设特快列车的平均速度为xkm/h，则高铁列车的平均速度为2．5xkm/h，关键描述语是：高铁列车的运行时间比特快列车所用的时间减少了16h，等量关系为：乘特快列车的行程1800km的时间=高铁列车的行驶860km的时间+16小时．

    试题解析：【解析】
    设特快列车的平均速度为xkm/h，

    由题意得：，

    解得：x=91，

    经检验：x=91是分式方程的解．

    答：特快列车的平均速度为91km/h．

    考点：分式方程的应用（行程问题）．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014年初中毕业升学考试（辽宁阜新卷）数学（解析版） 题型：填空题

    如图，是⊙O的内接三角形，如果，那么_______度．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（贵州黔西卷）数学（解析版） 题型：解答题

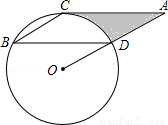
    如图，点B、C、D都在⊙O上，过C点作CA∥BD交OD的延长线于点A，连接BC，∠B=∠A=30°，BD=．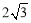

    （1）求证：AC是⊙O的切线；

    （2）求由线段AC、AD与弧CD所围成的阴影部分的面积．（结果保留π）

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（贵州黔西卷）数学（解析版） 题型：选择题

    已知两圆半径分别为3、5，圆心距为8，则这两圆的位置关系为（ ）

    A．外离 B．内含 C．相交 D．外切

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（贵州贵阳卷）数学（解析版） 题型：解答题

    如图，将一副直角三角形拼放在一起得到四边形ABCD，其中∠BAC=45°，∠ACD=30°，点E为CD边上的中点，连接AE，将△ADE沿AE所在直线翻折得到△AD′E，D′E交AC于F点．若AB=6cm．

    （1）AE的长为 cm；

    （2）试在线段AC上确定一点P，使得DP+EP的值最小，并求出这个最小值；

    （3）求点D′到BC的距离．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（贵州贵阳卷）数学（解析版） 题型：填空题

    若反比例函数的图象在其每个象限内，y随x的增大而增大，则k的值可以是 ．（写出一个k的值）

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（贵州贵阳卷）数学（解析版） 题型：选择题

    如图，在方格纸中，△ABC和△EPD的顶点均在格点上，要使△ABC∽△EPD，则点P所在的格点为（ ）

    A．P1 B．P2 C．P3 D．P4

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（贵州六盘水卷）数学（解析版） 题型：填空题

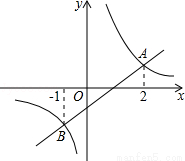
    如图，一次函数y1=k1x+b（k1≠0）的图象与反比例函数y2=k2x+b（k2≠0）的图象交于A，B两点，观察图象，当y1＞y2时，x的取值范围是　 　．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（福建南平卷）数学（解析版） 题型：解答题

    在图1、图2、图3、图4中，点P在线段BC上移动（不与B、C重合），M在BC的延长线上．

    （1）如图1，△ABC和△APE均为正三角形，连接CE．

    ①求证：△ABP≌△ACE．

    ②∠ECM的度数为　 　°．

    （2）①如图2，若四边形ABCD和四边形APEF均为正方形，连接CE．则∠ECM的度数为　 　°．

    ②如图3，若五边形ABCDF和五边形APEGH均为正五边形，连接CE．则∠ECM的度数为　 　°．

    （3）如图4，n边形ABC…和n边形APE…均为正n边形，连接CE，请你探索并猜想∠ECM的度数与正多边形边数n的数量关系（用含n的式子表示∠ECM的度数），并利用图4（放大后的局部图形）证明你的结论．

     

     

    查看答案和解析>>

    同步练习册答案