
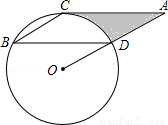
如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=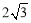 .
.
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
(1)证明见解析;(2)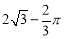 .
.
【解析】
试题分析:(1)连接OC,根据圆周角定理求出∠COA,根据三角形内角和定理求出∠OCA,根据切线的判定推出即可.
(2)求出DE,解直角三角形求出OC,分别求出△ACO的面积和扇形COD的面积根据转换思想,由即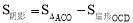 可得出答案.
可得出答案.
试题解析:【解析】
(1)证明:如答图,连接OC,交BD于E,
∵∠B和∠COD是同弧所对的圆周角和圆心角,∴∠COD=2∠B.
∵∠B=30°,∴∠COD=60°.
∵∠A=30°,∴∠OCA=90°,即OC⊥AC.∴AC是⊙O的切线.
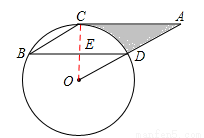
(2)∵AC∥BD,∠OCA=90°,∴∠OED=∠OCA=90°.
∵BD=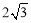 ,∴
,∴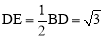 .
.
∵在Rt△ODE中,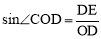 ,∴OD=2.
,∴OD=2.
∵在Rt△ACO中,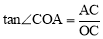 , ∴AC=
, ∴AC=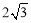 .
.
∴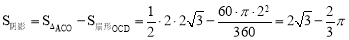 .
.
考点:1.圆周角定理;2.三角形内角和定理;3.切线的判定;4.平行线的性质;5.垂径定理;6.锐角三角函数定义;7.特殊角的三角函数值;8.扇形面积和三角形面积的计算;9.转换思想的应用.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源:2014年初中毕业升学考试(重庆A卷)数学(解析版) 题型:解答题
如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12.tan∠BAD= ,求sinC的值.
,求sinC的值.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(辽宁抚顺卷)数学(解析版) 题型:解答题
已知:Rt△A′BC′≌Rt△ABC,∠A′C′B=∠ACB=90°,∠A′BC′=∠ABC=60°,Rt△A′BC′可绕点B旋转,设旋转过程中直线CC′和AA′相交于点D.
(1)如图1所示,当点C′在AB边上时,判断线段AD和线段A′D之间的数量关系,并证明你的结论;
(2)将Rt△A′BC′由图1的位置旋转到图2的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°),当A、C′、A′三点在一条直线上时,请直接写出旋转角的度数.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(辽宁抚顺卷)数学(解析版) 题型:选择题
甲乙两地相距420千米,新修的高速公路开通后,在甲、乙两地行驶的长途客运车平均速度是原来的1.5倍,进而从甲地到乙地的时间缩短了2小时.设原来的平均速度为x千米/时,可列方程为( )
A. B.
B.
C. D.
D.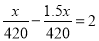
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:解答题
2014年12月26日,西南真正意义上的第一条高铁﹣贵阳至广州高速铁路将开始试运行,从贵阳到广州,乘特快列车的行程约为1800km,高铁开通后,高铁列车的行程约为860km,运行时间比特快列车所用的时间减少了16h.若高铁列车的平均速度是特快列车平均速度的2.5倍,求特快列车的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com