
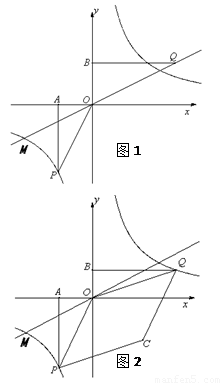
如图1,已知正比例函数和反比例函数的图象都经过点M(-2,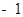 ),且P(
),且P(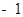 ,-2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
,-2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
(1)写出正比例函数和反比例函数的关系式;
(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?若存在,请求出点Q的坐标,若不存在,请说明理由;
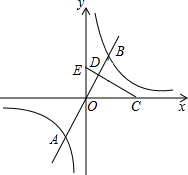
(3)如图2,当点Q在第一象限中的双曲线上运动时,作以 OP、OQ为邻边的平行四边形OPCQ,设点Q的横坐标为n,求平行四边形OPCQ周长(周长用n的代数式表示),并写出其最小值.
(1)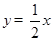 ,
, (2)
(2)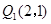 和
和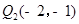 (3)
(3)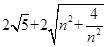 ,
,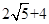
【解析】解:(1)正比例函数解析式为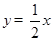 ---------------1分
---------------1分
反比例函数解析式为 ---------------2分
---------------2分
(2)当点Q在直线DO上运动时,
设点Q的坐标为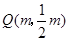 ,
----------------------3分
,
----------------------3分
于是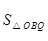 =
=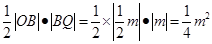
而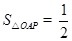 ×1×2=1
×1×2=1
所以有, ,解得
,解得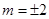 --------------------6分
--------------------6分
所以点Q的坐标为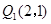 和
和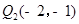 -------------------7分
-------------------7分
(3)因为四边形OPCQ是平行四边形,所以OP=CQ,OQ=PC,
因为点Q在第一象限中双曲线上,所以点Q的坐标为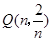 ,
,
由勾股定理可得,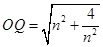 -------------------8分
-------------------8分
由勾股定理得OP=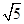 ,所以平行四边形OPCQ周长是
,所以平行四边形OPCQ周长是
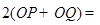
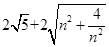 .····················· 10分
.····················· 10分
平行四边形OPCQ周长的最小值是 .-------11分
.-------11分
备注:
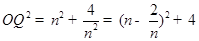
而点P(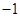 ,
,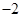 )是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值.
)是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值.
所以当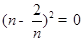 即
即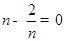 时,
时,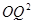 有最小值4,
有最小值4,
又因为OQ为正值,所以OQ与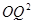 同时取得最小值,所以OQ有最小值2.
同时取得最小值,所以OQ有最小值2.
(1)正比例函数和反比例函数的图象都经过点M(-2,-1),设出正比例函数和反比例函数的解析式,运用待定系数法可求它们解析式;
(2)求得三角形OBQ和三角形OAP的面积进行解答
(3)因为四边形OPCQ是平行四边形,所以OP=CQ,OQ=PC,由勾股定理可得OQ,OP的长,而点P(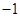 ,
,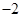 )是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值,所以当
)是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值,所以当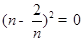 即
即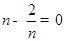 时,
时,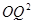 有最小值4,又因为OQ为正值,所以OQ与
有最小值4,又因为OQ为正值,所以OQ与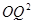 同时取得最小值,所以OQ有最小值2.
同时取得最小值,所以OQ有最小值2.


科目:初中数学 来源: 题型:
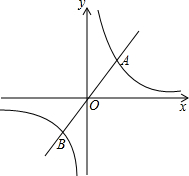 如图,已知正比例函数y=x与反比例函数y=
如图,已知正比例函数y=x与反比例函数y=| 1 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x |
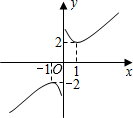 象似双钩,我们称之为“双钩函数”).给出下列几个命题:
象似双钩,我们称之为“双钩函数”).给出下列几个命题:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知正比例函数y=ax(a≠0)的图象与反比例函致y=
如图,已知正比例函数y=ax(a≠0)的图象与反比例函致y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•相城区一模)如图,已知正比例函数和反比例函数的图象都经过点M(-2,-1),且P(-1,-2)为双曲线上的一点.
(2012•相城区一模)如图,已知正比例函数和反比例函数的图象都经过点M(-2,-1),且P(-1,-2)为双曲线上的一点.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知正比例函数y1=x,反比例函数y2=
已知正比例函数y1=x,反比例函数y2=| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com