
分析 (1)提取公因式x得到x(x+1)=0,再解两个一元一次方程即可;
(2)利用直接开平方法解方程即可;
(3)把常数项移到等号右边,再进行配方,然后开方求出方程的解;
(4)提取公因式(x+3)得到x(x+3)(1-x)=0,再解两个一元一次方程即可;
(5)把x+3看成一个整体,符合完全平方式,直接开方.
解答 解:(1)∵x2+x=0,
∴x(x+1)=0,
∴x1=0,x2=-1;
(2)∵(x+1)2=4,
∴x+1=±2,
∴x1=1,x2=-3;
(3)∵x2-4x-4=1,
∴x2-4x+4=8+1,
∴(x-2)2=9,
∴x-2=±3,
∴x1=5,x2=-1;
(4)∵x+3-x(x+3)=0,
∴(x+3)(1-x)=0,
∴x+3=0或1-x=0,
∴x1=-3,x2=1;
(5)∵(x+3)2-10(x+3)+25=0,
∴(x+3-5)2=0,
∴(x-2)2=0,
∴x1=x2=2.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
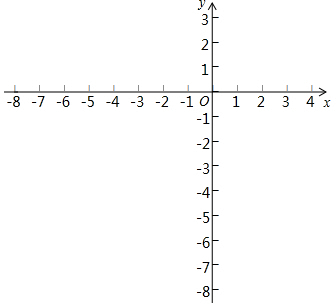 已知:平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
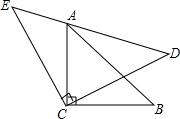 如图,在等腰直角三角形Rt△ABC和Rt△ECD中,Rt△ACB的顶点A在Rt△ECD的斜边ED上,求证:AE2+AD2=2AC2.(提示:添加辅助线连接BD)
如图,在等腰直角三角形Rt△ABC和Rt△ECD中,Rt△ACB的顶点A在Rt△ECD的斜边ED上,求证:AE2+AD2=2AC2.(提示:添加辅助线连接BD)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 四边形ABCD中,已知∠B=80°,∠C=60°,AP、DP分别平分∠BAD、∠ADC,则∠P的度数是( )
四边形ABCD中,已知∠B=80°,∠C=60°,AP、DP分别平分∠BAD、∠ADC,则∠P的度数是( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com