练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：关于x的一元二次方程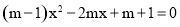（m>1）．

    （1）求证：方程总有两个不相等的实数根.

    （2）m为何整数时，此方程的两个实数根都为正整数？[]

     

    （1）证明见解析；（2）2或3.

    【解析】

    试题分析：（1）表示出根的判别式，得到根的判别式大于0，进而确定出方程总有两个不相等的实数根.

    （2）由（1）得到方程有两个不相等的实数根，利用求根公式表示出方程的两根：，要使原方程的根是整数，必须使得为正整数，则m-1=1或2，进而得出符合条件的m的值．

    试题解析：（1）∵，

    ∴方程总有两个不相等的实数根.分

    （2）∵，

    ∴由求根公式解得．

    ∵，方程的两个根都为正整数，m是整数且m>1.

    ∴是正整数．

    ∴或2．

    ∴或3．

    考点：1.一元二次方程根的判别式；2.一元二次方程的定义；3.解一元二次方程．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014年北京市海淀区中考二模数学试卷（解析版） 题型：计算题

    计算：

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市房山区中考一模数学试卷（解析版） 题型：解答题

    阅读下列材料：

    小明遇到这样一个问题：已知：在△ABC中，AB,BC,AC三边的长分别为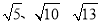，求△ABC的面积．

    小明是这样解决问题的：如图1所示，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），从而借助网格就能计算出△ABC的面积．他把这种解决问题的方法称为构图法．

    请回答：

    （1）图1中△ABC的面积为 ；

    参考小明解决问题的方法，完成下列问题：

    （2）图2是一个6×6的正方形网格(每个小正方形的边长为1) ．

    ①利用构图法在答题卡的图2中画出三边长分别为的格点△DEF；

    ②计算△DEF的面积为 ．

    （3）如图3，已知△PQR，以PQ，PR为边向外作正方形PQAF，PRDE，连接EF．若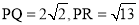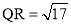， ,则六边形AQRDEF的面积为__________．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市房山区中考一模数学试卷（解析版） 题型：选择题

    将二次函数化为的形式，下列结果正确的是[（ ）]

    A． B．

    C． D．

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市怀柔区中考一模数学试卷（解析版） 题型：解答题

    在平面直角坐标系xOy中，二次函数的图象经过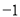（，0）和（，0）两点.

    （1）求此二次函数的表达式.

    （2）直接写出当＜x＜1时，y的取值范围.

    （3）将一次函数 y=(1-m)x+2的图象向下平移m个单位后，与二次函数图象交点的横坐标分别是a和b,其中a<2<b，试求m的取值范围.

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市怀柔区中考一模数学试卷（解析版） 题型：解答题

    已知：如图，点A、B、C在同一直线上，AD∥CE，AD=AC，∠D=∠CAE.

    求证：DB=AE.

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市怀柔区中考一模数学试卷（解析版） 题型：选择题

    在下列某品牌T恤的四个洗涤说明图案的设计中，没有运用旋转或轴对称知识的是（ ）

    A． B． C． D．

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市平谷区中考一模数学试卷（解析版） 题型：计算题

    计算：

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市东城区中考一模数学试卷（解析版） 题型：解答题

    已知：关于x的一元二次方程mx2﹣（4m+1）x+3m+3=0 （m＞1）．

    （1）求证：方程有两个不相等的实数根；

    （2）设方程的两个实数根分别为x1，x2（其中x1＞x2），若y是关于m的函数，且y=x1﹣3x2，求这个函数的解析式；

    （3）将（2）中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象回答：当关于m的函数y=2m+b的图象与此图象有两个公共点时，b的取值范围．

     

     

    查看答案和解析>>

    同步练习册答案