
阅读下列材料:
小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为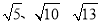 ,求△ABC的面积.
,求△ABC的面积.
小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法.
请回答:
(1)图1中△ABC的面积为 ;
参考小明解决问题的方法,完成下列问题:
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1) .
①利用构图法在答题卡的图2中画出三边长分别为 的格点△DEF;
的格点△DEF;
②计算△DEF的面积为 .
(3)如图3,已知△PQR,以PQ,PR为边向外作正方形PQAF,PRDE,连接EF.若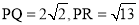 ,
,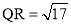 ,则六边形AQRDEF的面积为__________.
,则六边形AQRDEF的面积为__________.

(1)3.5;(2)①作图见解析;②8;(3)31.
【解析】
试题分析:(1)应用构图法,用四边形面积减去三个三角形面积即可得.
(2)①根据题意作出图形;②应用构图法,用四边形面积减去三个三角形面积即可得.
(3)如图,将△PQR绕点P逆时针旋转900,由于四边形PQAF,PRDE是正方形,故F,P,H共线,即△PEF和△PQR是等底同高的三角形,面积相等.
应用构图法,求出△PQR的面积: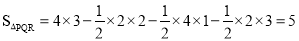 .
.
从而由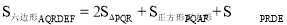 求得所求.
求得所求.
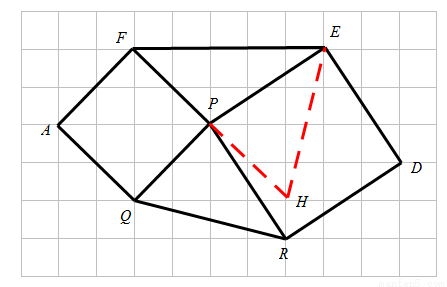
试题解析:(1)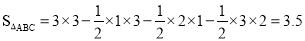 .
.
(2)①作图如下(答案不唯一):
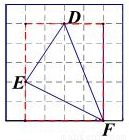
②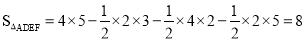 .
.
(3)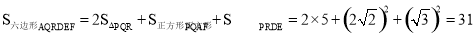 .
.
考点:1.设计和应用作图;2.网格问题;3.勾股定理;4.三角形面积的计算;5.旋转的性质;6.转换思想的应用.


科目:初中数学 来源:2014年北京市西城区中考二模数学试卷(解析版) 题型:解答题
已知关于 的一元二次方程x2+2x+3k-6=0有两个不相等的实数根
的一元二次方程x2+2x+3k-6=0有两个不相等的实数根
(1)求实数 的取值范围;
的取值范围;
(2)若 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:解答题
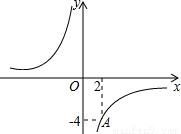
如图,点A在反比例函数 的图象上.
的图象上.
(1) 求反比例函数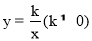 的解析式;
的解析式;
(2)在y轴上是否存在点P,使得△AOP是直角三角形?若存在,直接写出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:解答题
已知:关于x的一元二次方程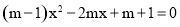 (m>1).
(m>1).
(1)求证:方程总有两个不相等的实数根.
(2)m为何整数时,此方程的两个实数根都为正整数?[]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com