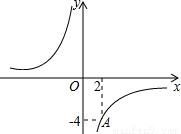
如图.点A在反比例函数的图象上.(1) 求反比例函数的解析式,(2)在y轴上是否存在点P.使得△AOP是直角三角形?若存在.直接写出P点坐标,若不存在.请说明理由．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，点A在反比例函数的图象上.

（1) 求反比例函数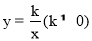的解析式；

（2）在y轴上是否存在点P，使得△AOP是直角三角形？若存在，直接写出P点坐标；若不存在，请说明理由．

（1）；（2）（0，-4）或（0，-5）．

【解析】

试题分析：（1）把A（2，-4）代入，即可求得k的值，从而求得函数的解析式.

（2）分∠OPA=90°和∠OAP=90°，两种情况进行讨论即可求解．

试题解析：：（1）把A（2，-4）代入得：，解得：k=-8.

则函数的解析式是：.

（2）当∠OPA=90°时，AP⊥y轴，则P的坐标是（0，-4）.

当∠OAP=90°时，根据OA2=4OP，则20=4OP，∴OP=5．则P的坐标是（0，-5）．

∴P的坐标是（0，-4）或（0，-5）．

考点：1.待定系数法求反比例函数解析式；2.反比例函数的性质；3.分类思想的应用．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：2014年北京市西城区中考二模数学试卷（解析版） 题型：填空题

如图，在平面直角坐标系xOy中，已知抛物线（0≤x≤3）在x轴上方的部分，记作C1，它与x轴交于点O，A1，将C1绕点A1旋转180°得C2，C2与x 轴交于另一点A2．请继续操作并探究：将C2绕点A2旋转180°得C3，与x 轴交于另一点A3；将C3绕点A 2旋转180°得C4，与x 轴交于另一点A4，这样依次得到x轴上的点A1，A2，A3，…，An，…，及抛物线C1，C2，…，Cn，…．则点A4的坐标为；Cn的顶点坐标为 (n为正整数，用含n的代数式表示) ．

查看答案和解析>>

科目：初中数学 来源：2014年北京市房山区中考二模数学试卷（解析版） 题型：解答题

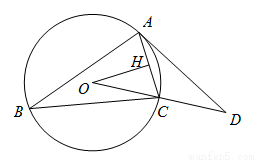
已知：如图，△ABC内接于⊙O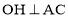，于H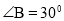，，过A点的直线与OC的延长线交于点D，，.

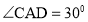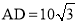（1）求证：AD是⊙O的切线；

（2）若E为⊙O上一动点，连接AE交直线OD于点P，问：是否存在点P,使得PA+PH的值最小，若存在求PA+PH的最小值，若不存在，说明理由.

查看答案和解析>>

科目：初中数学 来源：2014年北京市房山区中考二模数学试卷（解析版） 题型：选择题

从1．2． 3．4．5这五个数中随机取出一个数，取出的数是某个整数的平方数的概率是（）

A． B． C． D．

查看答案和解析>>

科目：初中数学 来源：2014年北京市房山区中考一模数学试卷（解析版） 题型：解答题

阅读下列材料：

小明遇到这样一个问题：已知：在△ABC中，AB,BC,AC三边的长分别为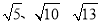，求△ABC的面积．

小明是这样解决问题的：如图1所示，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），从而借助网格就能计算出△ABC的面积．他把这种解决问题的方法称为构图法．

请回答：

（1）图1中△ABC的面积为；

参考小明解决问题的方法，完成下列问题：

（2）图2是一个6×6的正方形网格(每个小正方形的边长为1) ．

①利用构图法在答题卡的图2中画出三边长分别为的格点△DEF；

②计算△DEF的面积为．

（3）如图3，已知△PQR，以PQ，PR为边向外作正方形PQAF，PRDE，连接EF．若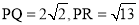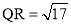， ,则六边形AQRDEF的面积为__________．

查看答案和解析>>

科目：初中数学 来源：2014年北京市房山区中考一模数学试卷（解析版） 题型：填空题

如图，点P1（x1，y1），点P2（x2，y2），…，点Pn（xn，yn）都在函数（x＞0）的图象上，△P1OA1，△P2A1A2，△P3A2A3，…，△PnAn﹣1An都是等腰直角三角形，斜边OA1，A1A2，A2A3，…，An﹣1An都在x轴上（n是大于或等于2的正整数），已知点A1的坐标为（2，0），则点P1的坐标为　　　　；点P2的坐标为　　　　；点Pn的坐标为　　　　　（用含n的式子表示）．