
【题目】如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.(1)求∠BAC的度数;(2)若∠DAC=45°,DC=8,求图中阴影部分的面积(保留π).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),若以B,O,C为顶点的三角形与△ABO全等,则点C的坐标不能为( )

A.(0,﹣4)B.(﹣2,0)C.(2,4)D.(﹣2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①已知:△ABC中,BC=m,∠A=60°.问满足此条件的三角形有多少个?它们的最大面积存在吗?若存在求出最大面积,并回答此时三角形的形状;若不存在,请说明理由.

②有一个正方形的养鱼塘,四个角各有一棵大树.生产队设想把鱼塘扩大,使它成为一个面积最大的正方形,而又不把树挖掉,这一设想能否实现?若能,请你设计画出图形,并证明此时面积最大.若不能,请说明理由.

③上问题推广,有一个正五边形的养鱼塘,五个角各有一棵树,要扩大使它成为面积最大的正五边形,而又不把树挖掉,可以吗?画图说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD的度数为__________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
(1)求证:△BCE≌△DCF;
(2)求CF的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等腰三角形,AB=AC,AB>BC,∠1=∠2≠90°,∠1+∠BAC=180°,点A、F、E、D在一条直线上,点D在BC边上,CD=2BD.若△ABC的面积为40,求△ABE与△CDF的面积之和________
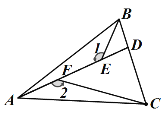
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com