
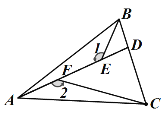
【题目】如图,△ABC为等腰三角形,AB=AC,AB>BC,∠1=∠2≠90°,∠1+∠BAC=180°,点A、F、E、D在一条直线上,点D在BC边上,CD=2BD.若△ABC的面积为40,求△ABE与△CDF的面积之和________
【答案】![]()
【解析】
先证明△ABE≌△CAF(AAS),再得到△ABE与△CDF的面积之和即为△ADC的面积,再求△ADC的面积即可.
∵∠1=∠2≠90°,∠1+∠BAC=180°,
∴∠2+∠BAC=180°,
又∵∠2+∠FAC+∠FCA=180°,
∴∠BAC=∠FAC+∠FCA,
又∵∠BAC=∠BAE+∠FAC,
∴∠BAE+∠FAC=∠FAC+∠FCA,
∴∠BAE=∠FCA,
在△ABE和△CAF中
 ,
,
∴△ABE≌△CAF(AAS),
∴△ABE与△CDF的面积之和为S△ADC。
∵点D在BC边上,CD=2BD.若△ABC的面积为40,
∴S△AD=![]() .
.
∴△ABE与△CDF的面积之和为![]()
故答案是:![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
(1)求顶点D的坐标(用含m的代数式表示);
(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线![]() 的位置,求平移的方向和距离;
的位置,求平移的方向和距离;
(3)当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广场上一个形状是平行四边形的花坛,分别种有红、黄、蓝、白、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是( )
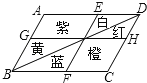
A.红花,白花种植面积一定相等
B.红花,蓝花种植面积一定相等
C.蓝花,黄花种植面积一定相等
D.紫花,橙花种植面积一定相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.(1)求∠BAC的度数;(2)若∠DAC=45°,DC=8,求图中阴影部分的面积(保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无人机技术我国逐渐发展迅速,全球首款吨位级货运无人机从设计到总装在四川成都双流区完成,现有两架航拍无人机:1号无人机从海拔5米处出发,以1米/秒的速度上升。与此同时,2号无人机从海拔15米处出发,以0.5米/秒的速度上升(设无人机上升时间为![]() 秒)。
秒)。
(1)求出1号无人机所在位置的海拔![]() (米)与
(米)与![]() 之间的关系式和2号无人机所在位置的海拔
之间的关系式和2号无人机所在位置的海拔![]() (米)与
(米)与![]() 之间的关系式?
之间的关系式?
(2)在某一时刻两架无人机能否位于同一高度?如果能,请求出无人机上升的时间与高度?如果不能,请说明理由.
(3)上升多少时间,两架无人机所在位置的海拔相差5米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
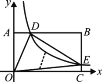
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间的甲、乙两名工人分别同时生产同种零件,在开始生产的前2个小时为生产磨合期,2个小时后有一人停工一段时间对设备进行改良升级,以提升生产效率,另一人进入正常的生产模式,他们每人生产的零件总数![]() (个)与生产时间
(个)与生产时间![]() (小时)的关系如图所示,根据图象回答:
(小时)的关系如图所示,根据图象回答:
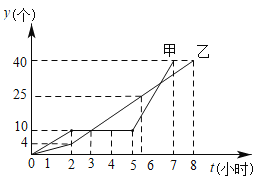
(1)在生产过程中,哪位工人对设备进行改良升级,停止生产多少小时?
(2)当![]() 为多少时,甲、乙所生产的零件个数第一次相等?甲、乙中,谁先完成一天的生产任务?
为多少时,甲、乙所生产的零件个数第一次相等?甲、乙中,谁先完成一天的生产任务?
(3)设备改良升级后每小时生产零件的个数是多少?与另一工人的正常生产速度相比每小时多生产几个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com