
【题目】如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,DE=DF,连接AD.
求证:(1)∠FAD=∠EAD;
(2)BD=CD.

【答案】(1)证明见解析;证明见解析.
【解析】试题分析:(1)根据BE⊥AC、CF⊥AB,DE=DF可直接得出AD是∠BAC的平分线,由角平分线的定义可知∠FAD=∠EAD;
(2)由DE=DF,AD=AD可知Rt△ADF≌Rt△ADE,故可得出∠ADF=∠ADE,由对顶角相等可知∠BDF=∠CDE,进而可得出∠ADB=∠ADC,由以上条件可判断出△ABD≌△ACD,由全等三角形的判定定理即可得出BD=CD.
试题解析:证明:(1)∵BE⊥AC、CF⊥AB,DE=DF,
∴AD是∠BAC的平分线,
∴∠FAD=∠EAD;
(2)∵△ADF与△ADE是直角三角形,DE=DF,AD=AD,
∴Rt△ADF≌Rt△ADE,
∴∠ADF=∠ADE,
∵∠BDF=∠CDE,
∴∠ADF+∠BDF=∠ADF+∠CDE,
即∠ADB=∠ADC,
在△ABD≌△ACD中,
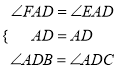 ,
,
∴△ABD≌△ACD,
∴BD=CD.


科目:初中数学 来源: 题型:
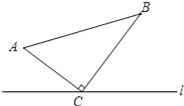
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=_________秒时,△PEC与△QFC全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠B=90°,
(1)根据要求作图(尺规作图,保留作图痕迹,不写画法):
①作∠BAC的平分线AD交BC于D;
②作线段AD的垂直平分线交AB于E,交AC于F,垂足为H;
③连接ED.
(2)在(1)的基础上写出一对全等三角形:△ ≌△ 并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a=123456789×987654321,b=123456788×987654322,则下列各式正确的是( )
A. a>b B. a<b C. a=b D. 不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com