
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.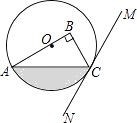
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
【答案】
(1)解:MN是⊙O切线.
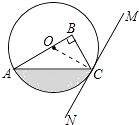
理由:连接OC.
∵OA=OC,
∴∠OAC=∠OCA,
∵∠BOC=∠A+∠OCA=2∠A,∠BCM=2∠A,
∴∠BCM=∠BOC,
∵∠B=90°,
∴∠BOC+∠BCO=90°,
∴∠BCM+∠BCO=90°,
∴OC⊥MN,
∴MN是⊙O切线.
(2)解:由(1)可知∠BOC=∠BCM=60°,
∴∠AOC=120°,
在Rt△BCO中,OC=OA=4,∠BCO=30°,
∴BO= ![]() OC=2,BC=2
OC=2,BC=2 ![]()
∴S阴=S扇形OAC﹣S△OAC= ![]() ﹣
﹣ ![]() =
= ![]() ﹣4
﹣4 ![]() .
.
【解析】(1)要证直线MN与⊙O的切线,连接OC.易证∠BOC=2∠A,由∠BCM=2∠A,得出∠BOC=∠BCM,在Rt△OBC中,根据直角三角形两锐角互余,可推出OC⊥MN,即可得出结论。
(2)先求出∠AOC的度数,在Rt△BCO中,利用解直角三角形求出BO、BC的长,根据S阴=S扇形OAC﹣S△OAC,即可求出阴影部分的面积。


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,⊿ABC的顶点在格点上。 且A(1,-4),B(5,-4),C(4,-1)
【1】画出⊿ABC;
【1】求出⊿ABC 的面积;![]()
【1】若把⊿ABC向上平移2个单位长度,再向左平移4个单位长度得到⊿![]()
![]() B
B![]() C
C![]() ,在图中画出⊿
,在图中画出⊿![]()
![]() B
B![]() C
C![]() ,并写出B
,并写出B![]() 的坐标。
的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
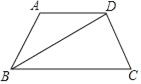
【题目】如图,四边形ABCD中,AD∥BC,∠A=120°,BD平分∠ABC.
(1)若BD⊥CD,求∠C的度数;
(2)射线AP从AB位置开始,以每秒10°的速度绕点A逆时针旋转,6秒后AP与BD有何种位置关系?并说明理由.
(3)在(2)的条件下,AP旋转一圈回到AB处时停止运动,若射线AP与直线BD相交所成的角中较小的角为x°,当10<x<20,则旋转时间t(单位:秒)的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0)、B(4,1)两点,且与y轴交于点C.
(1)求抛物线的解析式;
(2)如图(1),设抛物线与x轴的另一个交点为D,在抛物线的对称轴上找一点H,使△CDH的周长最小,求出H点的坐标并求出最小周长值.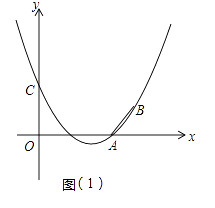
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合),经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求面积的最小值及E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的顶点A、C在双曲线y1=﹣ ![]() 上,B、D在双曲线y2=
上,B、D在双曲线y2= ![]() 上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= . 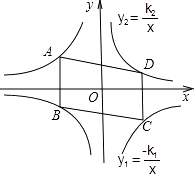
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式 ![]() 成立的一对有理数
成立的一对有理数![]() ,
,![]() 为“共生有理数对”,记为(
为“共生有理数对”,记为(![]() ,
,![]() ),如:数对(
),如:数对(![]() ,
,![]() ),(
),(![]() ,
,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(![]() ,
,![]() ),(
),(![]() ,
,![]() )中是“共生有理数对”吗?说明理由.
)中是“共生有理数对”吗?说明理由.
(2)若(![]() ,
,![]() )是“共生有理数对”,则(
)是“共生有理数对”,则(![]() ,
,![]() )是“共生有理数对”吗?说明理由.
)是“共生有理数对”吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.
方案一:每千克种子价格为4元,均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.
(1)请分别求出方案一、方案二中购买的种子数量x(千克)与付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里,有5个除颜色外,其他都相同的小球,其中有3个是红球,2个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
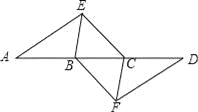
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com