
【题目】已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.

(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为 .
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.(可用备用图)
(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G.将∠AEG绕点A顺时针旋转30°得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′,C′分别在直线l2,l4上,求菱形AB′C′D′的边长.


【答案】(1)![]()
(2)![]() ,
, ![]()
(3)![]()
【解析】试题分析: (1)利用已知得出△AED≌△DGC(AAS),即可得出AE,以及正方形的边长;
(2)如图2过点B作BE⊥L1于点E,反向延长BE交L4于点F,则BE=1,BF=3,由四边形ABCD是矩形,∠ABC=90°,∠ABE+∠FBC=90°,根据∠ABE+∠EAB=90°,得到∠FBC=∠EAB,然后分类讨论,求得矩形的宽.
(3)首先过点E′作ON垂直于l1分别交l1,l2于点O,N,∠AEO=30°,则∠ED′N=60°,可求出AE=1,EO,EN,ED′的长,进而由勾股定理可知菱形的边长.
解:(1)∵l1∥l2∥l3∥l4,∠AED=90°
∴∠DGC=90°,
∵四边形ABCD为正方形
∴∠ADC=90°,AD=CD,∵∠ADE+∠2=90°,
∴∠1+∠2=90°,
∴∠1=∠ADE,
∵l3∥l4
∴∠1=∠DCG,
∠ADE=∠DCG,
在△AED与△DGC中,
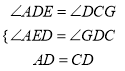 ,
,
∴△AED≌△GDC(AAS),
∴AE=GD=1,ED=GC=3,
∴AD=![]() ,
,
故答案为: ![]() ;
;
(2)如图2过点B作BE⊥L1于点E,反向延长BE交L4于点F,
则BE=1,BF=3,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABE+∠FBC=90°,
∵∠ABE+∠EAB=90°,
∴∠FBC=∠EAB,
当AB<BC时,AB=![]() BC,
BC,
∴AE=![]() BF=
BF=![]() ,
,
∴AB=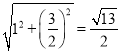 ;
;
如图3当AB>BC时,
同理可得:BC=![]() ,
,
∴矩形的宽为: ![]() ,
, ![]() ;
;
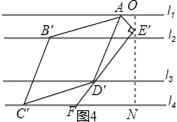
(3)如图4过点E′作ON垂直于l1分别交l1,l4于点O,N,
∵∠OAE′=30°,则∠E′FN=60°
∵AE′=AE=1,
故E′O=![]() ,E′N=
,E′N=![]() ,E′D′=
,E′D′=![]() ,
,
由勾股定理可知菱形的边长为: ![]() .
.





科目:初中数学 来源: 题型:
【题目】尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于![]() CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
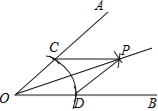
A. SAS B. ASA C. AAS D. SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①a为任意有理数,a2+1总是正数;②如果a+|a|=0,则a<0;③两点确定一条直线;④若MA=MB,则点M是线段AB的中点.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有三个球,其中2个红球,1个白球,它们除颜色不同外其余都相同:
(1)摸出一个球记下颜色后放回,并搅匀,再摸出一个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(2)现再将n个白球放入布袋中搅匀后使摸出一个球是白球的概率为![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作试验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(-1,3),C(-3,2)
(1)作出△ABC关于x轴对称的△![]() ;
;
(2)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;
的坐标为 ;
(3)点P(a,a-2)与点Q关y轴对称,若PQ=8,则点P的坐标为 ;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
学习了三角形全等的判定方法(即“SSS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
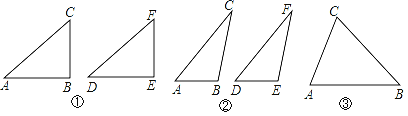
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,请你证明:△ABC≌△DEF(提示:过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H).
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你利用图③,在图③中用尺规作出△DEF,使△DEF和△ABC不全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com