
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随着点
的位置随着点![]() 的位置变化而变化.
的位置变化而变化.

(1)如图1,当点![]() 在四边形
在四边形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是________,
的数量关系是________,![]() 与
与![]() 的位置关系是_______;
的位置关系是_______;
(2)如图2,当点![]() 在四边形
在四边形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;
外部时,(1)中的结论是否还成立?若成立,请予以证明;
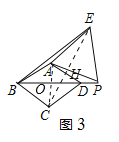
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,则线段
,则线段![]() ______,
______,![]() ________.
________.
【答案】(1)PB=EC,CE⊥AD;(2)结论仍然成立,理由见解析;(3)DP= 10,EP=![]()
【解析】
(1)如图1中,结论:PB=EC,CE⊥AD.连接AC,延长CE交AD于H,根据“SAS”证明△BAP≌△CAE即可解决问题;
(2)结论仍然成立.连接AC交BD于O,设CE交AD于H.证明方法与(1)类似;
(3)首先证明△BAP≌△CAE,解直角三角形求出AP,DP,OA即可解决问题;
解:(1)如图1中,结论:PB=EC,CE⊥AD.
理由:连接AC,延长CE交AD于H.
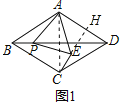
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∵∠BAC=∠PAE,
∴∠BAP=∠CAE,
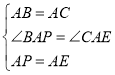 ,
,
∴△BAP≌△CAE,
∴BP=CE,∠ABP=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD.
故答案为PB=EC,CE⊥AD;
(2)结论仍然成立.
理由:选图2,连接AC交BD于O,设CE交AD于H.
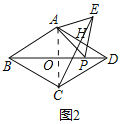
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∴∠BAP=∠CAE.
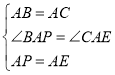 ,
,
∴△BAP≌△CAE,
∴BP=CE,∠PBA=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD.
(3)选图3,连接AC交BD于O,连接CE交AD于H.
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∴∠BAP=∠CAE.
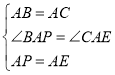 ,
,
∴△BAP≌△CAE,
∴BP=CE,∠ABP=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,即CE⊥AD.
在菱形ABCD中,AD∥BC,
∴EC⊥BC,
∵BC=AB=2![]() ,BE=
,BE=![]() ,
,
在Rt△BCE中,EC=![]() =7,
=7,
∴BP=CE=7,
∵AC与BD是菱形的对角线,
∴∠ABD=![]() ∠ABC=30°,AC⊥BD,
∠ABC=30°,AC⊥BD,
∴OA=![]() AB=
AB=![]() ,
,
∴BO=OD=![]() =3,
=3,
∴BD=2BO=6,
∴DP=BP-BD=7-6=1,
∴OP=OD+DP=4,
在Rt△AOP中,AP=![]() ,
,
∴EP=AP=![]() .
.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图(a),直线l1:y=kx+b经过点A、B,OA=OB=3,直线12:y=![]() x﹣2交y轴于点C,且与直线l1交于点D,连接OD.
x﹣2交y轴于点C,且与直线l1交于点D,连接OD.

(1)求直线11的表达式;
(2)求△OCD的面积;
(3)如图(b),点P是直线11上的一动点;连接CP交线段OD于点E,当△COE与△DEP的面积相等时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
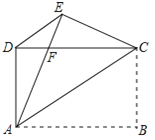
(1)求证:△DEC≌△EDA;
(2)求DF的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)
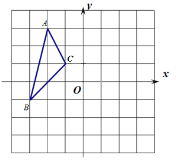
(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
【答案】(1)作图见解析,(-4,-2);(2)作图见解析,(2,-3);(3)相等.
【解析】
试题分析:(1)根据旋转的性质作图,写出点的坐标;
根据旋转的性质作图,写出点的坐标;
(3)根据旋转的性质得出结论.
试题解析:(1)作图如下,点A1的坐标(-4,-2).
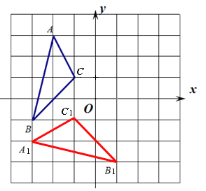
(2)作图如下,点A2的坐标(2,-3).
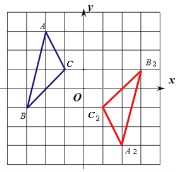
(3)相等.
考点:1.旋转作图;2.旋转的性质.
【题型】解答题
【结束】
20
【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个函数:
①y=kx(k为常数,k>0)
②y=kx+b(k,b为常数,k>0)
③y=![]() (k为常数,k>0,x>0)
(k为常数,k>0,x>0)
④y=ax2(a为常数,a>0)
其中,函数y的值随着x值得增大而减少的是( )
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在直角坐标平面中,点![]() 在
在![]() 轴的负半轴上,直线
轴的负半轴上,直线![]() 经过点
经过点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 是点
是点![]() 关于原点的对称点,过点
关于原点的对称点,过点![]() 的直线
的直线![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,如果
,如果![]() .
.
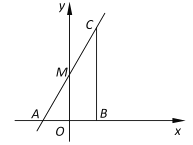
(1)求直线![]() 的表达式;
的表达式;
(2)如果点![]() 在直线
在直线![]() 上,且
上,且![]() 是等腰三角形,请求出点
是等腰三角形,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用图1中四个完全一样的直角三角形可以拼成图2的大正方形。

解答下列问题:
(1)请用含![]() 、
、![]() 、
、![]() 的代数式表示大正方形的面积.
的代数式表示大正方形的面积.
方法1: ;方法2: .
(2)根据图2,利用图形的面积关系,推导![]() 、
、![]() 、
、![]() 之间满足的关系式.
之间满足的关系式.
(3)利用(2)的关系式解答:如果大正方形的面积是25,且![]() ,求小正方形的面积.
,求小正方形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com