
【题目】用图1中四个完全一样的直角三角形可以拼成图2的大正方形。

解答下列问题:
(1)请用含![]() 、
、![]() 、
、![]() 的代数式表示大正方形的面积.
的代数式表示大正方形的面积.
方法1: ;方法2: .
(2)根据图2,利用图形的面积关系,推导![]() 、
、![]() 、
、![]() 之间满足的关系式.
之间满足的关系式.
(3)利用(2)的关系式解答:如果大正方形的面积是25,且![]() ,求小正方形的面积.
,求小正方形的面积.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)1.
;(3)1.
【解析】
(1)方法1、根据正方形面积公式求出即可;
方法2、根据大正方形面积等于4个直角三角形面积加小正方形的面积,即可得出答案;
(2)根据大正方形面积相等,即可得出等式;
(3)由大正方形的面积是25可得![]() =25,利用完全平分公式,可得
=25,利用完全平分公式,可得![]() ,则2ab=24,根据小正方形的面积
,则2ab=24,根据小正方形的面积![]() ,即可解答.
,即可解答.
解:(1)方法1:大正方形的边长是![]() ,面积是
,面积是![]() ,
,
方法2:大正方形面积等于4个直角三角形面积加小正方形的面积,即![]() ;
;
(2)![]() =
=![]()
![]() =
=![]()
![]() ;
;
(3)∵正方形的面积是25,
∴![]() =25,
=25,
∵![]()
∴![]() ,2ab=24,
,2ab=24,
∴小正方形的面积:![]() =25-24=1.
=25-24=1.
故答案为:(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)1.
;(3)1.


科目:初中数学 来源: 题型:
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随着点
的位置随着点![]() 的位置变化而变化.
的位置变化而变化.

(1)如图1,当点![]() 在四边形
在四边形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是________,
的数量关系是________,![]() 与
与![]() 的位置关系是_______;
的位置关系是_______;
(2)如图2,当点![]() 在四边形
在四边形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;
外部时,(1)中的结论是否还成立?若成立,请予以证明;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,则线段
,则线段![]() ______,
______,![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已如直线![]() ∥
∥![]() ,且
,且![]() 与
与![]() 、
、![]() 分别交于A、B两点,
分别交于A、B两点,![]() 与
与![]() 、
、![]() 分别交于C、D两点,记∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,点P在线段AB上.
分别交于C、D两点,记∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,点P在线段AB上.
(1)若∠1=25°,∠2=33°,则∠3=__________;
(2)猜想∠1,∠2,∠3之间的相等关系,并说明理由;
(3)如图2,点在点B的南偏东23°方向,在点C的西南方向,利用(2)的结论,可知∠BAC=__________;
(4)点P在直线![]() 上且在A、B两点外侧运动时,其它条件不变,请直接写出∠1,∠2,∠3之间的相等关系.
上且在A、B两点外侧运动时,其它条件不变,请直接写出∠1,∠2,∠3之间的相等关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 在线段
在线段![]() 上,
上,![]() 与
与![]() 交于点
交于点![]() ,
,![]() .求证:
.求证:![]() .(完成以下填空)
.(完成以下填空)
证明:∵![]() (已知),
(已知),
且![]() ( )
( )
∴![]() (等量代换)
(等量代换)
∴ ![]() ( )
( )
∴![]() ( )
( )
又∵![]() (已知)
(已知)
∴![]() (等量代换)
(等量代换)
∴![]() ( )
( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
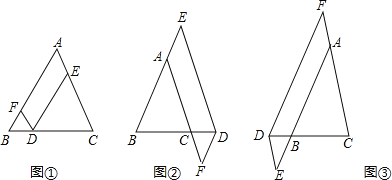
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示. AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601, ![]() ≈1.414].
≈1.414].

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AC=16,则图中长度为8的线段有( )

A. 2条 B. 4条 C. 5条 D. 6条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由49个边长为1的小正方形组成的7×7的正方形网格,小正方形的顶点为格点,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均在格点上.
均在格点上.

(1)直接写出![]() ________;
________;
(2)点![]() 在网格中的格点上,且
在网格中的格点上,且![]() 是以
是以![]() 为顶角顶点的等腰三角形,则满足条件的点
为顶角顶点的等腰三角形,则满足条件的点![]() 有________个;
有________个;
(3)请在如图所示的网格中,借助矩形![]() 和无刻度的直尺作出
和无刻度的直尺作出![]() 的角平分线,并保留作图痕迹.
的角平分线,并保留作图痕迹.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com