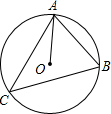
如图所示.⊙O是△ABC的外接圆.已知∠B=70°.则∠CAO的度数是( )A．20°B．30°C．35°D．40° 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

16．

如图所示，⊙O是△ABC的外接圆，已知∠B=70°，则∠CAO的度数是（　　）

A．

20°

B．

30°

C．

35°

D．

40°

分析延长AO交圆于点D，连接CD，先由直径所对的圆周角为90°，可得∠ACD=90°，然后由同弧所对的圆周角相等可得：∠D=∠B=70°，然后根据三角形内角和定理即可求出∠CAO的度数．

解答解：延长AO交圆于点D，连接CD，如图所示，

∵AD是直径，
∴∠ACD=90°，
∵∠D=∠B，∠B=70°，
∴∠D=70°，
∵∠ACD+∠D+∠CAO=180°，
∴∠CAO=180°-70°-90°=20°，
故选：A．

点评此题考查了圆周角定理：同弧所对的圆周角相等、直径所对的圆周角为90°及三角形内角和定理，解题的关键是：添加辅助线，体现转化的思想．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

6．判断由线段a，b，c组成的三角形是不是直角三角形．
（1）a=8，b=15，c=17；
（2）a=2，b=$\sqrt{13}$，c=3．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．

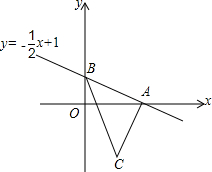如图，已知直线y=-$\frac{1}{2}$x+1与坐标轴交于A、B两点，C（1，-2），点P在y轴的负半轴上，且S_△PAB=S_△ABC．
（1）点A的坐标是（2，0），点B的坐标是（0，1）；
（2）求点P的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

4．

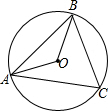如图，AB是圆形人工湖上的一座桥，桥长100米，在湖岸上一点C，测得∠ACB=60°，则这个人工湖的直径为（　　）

A．

50$\sqrt{3}$

B．

$\frac{100}{3}$$\sqrt{3}$

C．

$\frac{200}{3}$$\sqrt{3}$

D．

200$\sqrt{3}$

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．

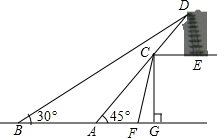如图为某风景区中古塔，大坝和湖的截面图，大坝顶端CE和水面平行，点C为大坝顶端拐角处，大坝的坡比i=3：1（即CG：FG=3：1），当小明和同伴从大坝的点F处沿着截面所在方向开始划船，划行20米到达点A处时，他们以仰角45°观察远方，正好看到古塔顶端的点D，且点C在视线AD上，当他们从点A继续沿原方向划船40米，到达点B处时，观察点D的仰角正好为30°．
（1）求大坝倾斜段上CF的长；（精确到0.1米，$\sqrt{10}$≈3.16）
（2）求古塔DE的高度．（精确到0.1米，$\sqrt{3}$≈1.73）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．

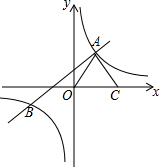如图，直线y=k₁x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A（1，3）、B（m，-1）两点．
（1）求直线和双曲线的解析式；
（2）观察图象，请直接写出不等式y=k₁x+b＞$\frac{{k}_{2}}{x}$的解集；
（3）点C为x轴正半轴上一点，连接AO、AC，且AO=AC，求S_△AOC．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．

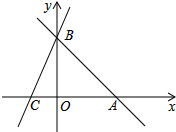直线CB：y=3x+b分别与x，y轴交于C（-2，0），B两点，过点B的直线交x轴正半轴于点A，且OB=OA．
（1）求直线AB的解析式；
（2）直线EF：y=kx-k（k≠0）交AB于点E，交BC于点F，交x轴于点D，是否存在这样的直线EF，使得S_△EBD=S_△FBD？若存在，求出k的值；若不存在，说明理由；
（3）动点M从点C出发沿x轴向点A运动，运动的速度为每秒1个单位长度，设M运动t s．
①当BM=CM时，求t的值；
②动点N从点A出发沿线段AB向点B运动，运动的速度为每秒$\frac{3}{4}$$\sqrt{2}$个单位长度，M，N两点同时出发，当其中一个动点到达终点时，它们都停止运动，当△MON为直角三角形时，求t的值．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

5．