
【题目】为实施乡村振兴战略,解决某山区老百娃出行难的问题,当地政府决定修建一条高速公路,其中一段长为146米的山体隧道贯穿工程由甲、乙两个工程队负责施工,甲工程队独立工作2天后,乙工程队加入,两个工程队又联合工作了1天,这3天共掘进26米,已知甲工程队平均每天比乙工程队多掘进2米.
(1)求甲、乙两个工程队平均每天分别掘进多少米?
(2)若甲、乙两个工程队按此施工速度进行隧道贯穿工程,剩余工程由这两个工程队联合施工,求完成这项隧道贯穿工程一共需要多少天?
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:
【题目】三江夜游项目是宁波市月光经济和“三江六岸”景观提升的重要工程,一艘游轮从周宿夜江游船码头到宁波大剧院游船码头顺流而行用40分钟,从宁波大剧院游船码头沿原线返回周宿夜江游船码头用了1小时,已知游轮在静水中的平均速度为8千米/小时,求水流的速度.设水流的速度为x千米/小时,则可列方程为( )
A.40(8-x)=1×(8+x) B.![]() (8+x)=8 C.
(8+x)=8 C.![]() (8+x)=8-x D.
(8+x)=8-x D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为拓宽销售渠道,某水果商店计划将146个柚子和400个橙子装入大、小两种礼箱进行出售,其中每件小礼箱装2个柚子和4个橙子;每件大礼箱装3个柚子和9个橙子.要求每件礼箱都装满,柚子恰好全部装完,橙子有剩余,设小礼箱的数量为x件.
(1)大礼箱的数量为________件(用含x的代数式表示).
(2)若橙子剩余12个,则需要大、小两种礼箱共多少件?
(3)由于橙子有剩余,则小礼箱至少需要________件.
查看答案和解析>>
科目:初中数学 来源: 题型:
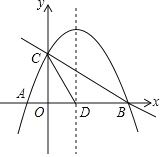
【题目】如图,抛物线![]() 与x轴交于
与x轴交于![]() 、B两点,与y轴交于点
、B两点,与y轴交于点![]() ,抛物线的对称轴交x轴于点D.
,抛物线的对称轴交x轴于点D.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 求
求![]() 的值;
的值;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
![]() 点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
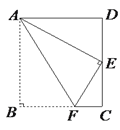
【题目】如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处, 折痕为AF,若CD=6,则AF等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有![]() 六个点,点
六个点,点![]() 在原点位置,点
在原点位置,点![]() 表示的数为
表示的数为![]() ,已知下表中
,已知下表中![]() 的含义均为前一个点所表示的数与后一个点所表示的数的差,比如
的含义均为前一个点所表示的数与后一个点所表示的数的差,比如![]() 为
为![]() .
.
|
|
|
|
|
|
|
|
|
|
若点![]() 与点
与点![]() 的距离为
的距离为![]() ,则
,则![]() 的值为________
的值为________
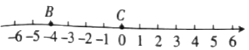
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是学习初中数学的- -个重要工具利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:数轴上点![]() 、点
、点![]() 表示的数为
表示的数为![]() ,则
,则![]() 两点之间的距离
两点之间的距离![]() ,若
,若![]() ,则可简化为;
,则可简化为;![]() 线段
线段![]() 的中点
的中点![]() 表示的数为
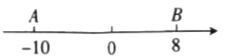
表示的数为![]() 如图,已知数轴上有
如图,已知数轴上有![]() 两点,分别表示的数为
两点,分别表示的数为![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度沿数轴向右匀速运动,点
个单位长度的速度沿数轴向右匀速运动,点![]() 以每秒
以每秒![]() 个单位长度向左匀速运动,设运动时间为
个单位长度向左匀速运动,设运动时间为![]() 秒
秒![]() .
.
(1)运动开始前,![]() 两点的距离为多少个单位长度;线段
两点的距离为多少个单位长度;线段![]() 的中点
的中点![]() 所表示的数为?
所表示的数为?
(2)点![]() 运动
运动![]() 秒后所在位置的点表示的数为 ;点
秒后所在位置的点表示的数为 ;点 ![]() 运动
运动![]() 秒后所在位置的点表示的数为 . (用含
秒后所在位置的点表示的数为 . (用含![]() 的式子表示
的式子表示
(3)它们按上述方式运动,![]() 两点经过多少秒会相距
两点经过多少秒会相距![]() 个单位长度?
个单位长度?
(4)若![]() 按上述方式运动,
按上述方式运动, ![]() 两点经过多少秒,线段
两点经过多少秒,线段![]() 的中点
的中点![]() 与原点重合?
与原点重合?
查看答案和解析>>
科目:初中数学 来源: 题型:
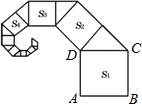
【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
A. (![]() )2013B. (
)2013B. (![]() )2014C. (
)2014C. (![]() )2013D. (
)2013D. (![]() )2014
)2014
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com